Generalized quaternion interpolation
Encyclopedia
Generalized quaternion interpolation is an interpolation
method that extends the quaternion slerp algorithm. This generalized method can interpolate between more than two unit-quaternion
s, but is neither closed-form
nor fixed-time
.
with weights 
is defined as the value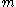 
that solves the sum
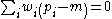and 
Because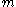
and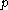 
values are unconstrained, this can be rewritten in the more familiar form of
Unit quaternions, on the other hand, are constrained and the closed-form interpolation solution can not be applied to them.
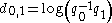
where the logarithm is the hypercomplex logarithm. This difference can be applied to the value in which it is a tangent-space member as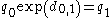
where the hypercomplex exponential is used.
With these definitions in mind, the quaternion interpolation of values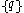
with weights 
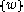can be defined (nearly identically to the unconstrained mean) as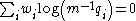
which says that the weighted sum of all differences to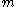
(in 
's tangent-space) is zero.
Each iteration of the algorithm is as follows, with an initial mean estimate of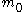
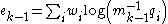
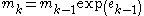
as iteration index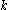
increases, the value 
will approach the true weighted-mean of the points.
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
method that extends the quaternion slerp algorithm. This generalized method can interpolate between more than two unit-quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s, but is neither closed-form
Closed-form expression
In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
nor fixed-time
Time complexity
In computer science, the time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the size of the input to the problem. The time complexity of an algorithm is commonly expressed using big O notation, which suppresses multiplicative constants and...
.
Definition of unconstrained interpolation
General interpolation of unconstrained values with weights is defined as the value 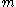that solves the sum 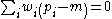and Because
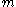and 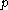values are unconstrained, this can be rewritten in the more familiar form ofUnit quaternions, on the other hand, are constrained and the closed-form interpolation solution can not be applied to them.
Conversion to constrained interpolation
Because the unit-quaternion space is a closed Riemannian manifold, the difference between any two values on the manifold (in the tangent-space of the first value) can be defined as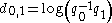where the logarithm is the hypercomplex logarithm. This difference can be applied to the value in which it is a tangent-space member as
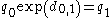
where the hypercomplex exponential is used.
With these definitions in mind, the quaternion interpolation of values
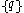with weights 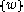can be defined (nearly identically to the unconstrained mean) as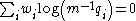which says that the weighted sum of all differences to
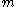(in 's tangent-space) is zero.Recursive formulation
The quaternion mean value defined above can be found in a recursive algorithm with some initial estimate (one of the points, for example) that will halt when the net-error is below some threshold or the algorithm has iterated beyond some time limit.Each iteration of the algorithm is as follows, with an initial mean estimate of
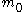
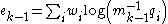
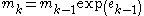
as iteration index
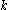increases, the value will approach the true weighted-mean of the points.