
Geodetic effect
Encyclopedia
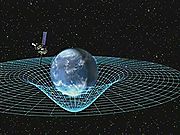
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
, predicted by general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, on a vector carried along with an orbiting body. For example, the vector could be the angular momentum of a gyroscope orbiting the earth, as carried out by the Gravity Probe B
Gravity Probe B
Gravity Probe B is a satellite-based mission which launched on 20 April 2004 on a Delta II rocket. The spaceflight phase lasted until 2005; its aim was to measure spacetime curvature near Earth, and thereby the stress–energy tensor in and near Earth...
experiment. The geodetic effect was first predicted by Willem de Sitter
Willem de Sitter
Willem de Sitter was a Dutch mathematician, physicist and astronomer.-Life and work:Born in Sneek, De Sitter studied mathematics at the University of Groningen and then joined the Groningen astronomical laboratory. He worked at the Cape Observatory in South Africa...
in 1916, who provided relativistic corrections to the Earth-Moon system's motion. De Sitter's work was extended in 1918 by Jan Schouten and in 1920 by Adriaan Fokker
Adriaan Fokker
Adriaan Daniël Fokker , was a Dutch physicist and musician.Fokker was born in Buitenzorg, Dutch East Indies ; he was a cousin of the aeronautical engineer Anthony Fokker...
.
It can also be applied to a particular secular precession
Precession
Precession is a change in the orientation of the rotation axis of a rotating body. It can be defined as a change in direction of the rotation axis in which the second Euler angle is constant...
of astronomical orbits, equivalent to the rotation of the Laplace–Runge–Lenz vector.
The term geodetic effect has two slightly different meanings as the moving body may be spinning or non-spinning. Non-spinning bodies move in geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s, whereas spinning bodies move in slightly different orbits.
The difference between de Sitter precession and Lense–Thirring precession (frame dragging) is that the de Sitter effect is due simply to the presence of a central mass, whereas Lense–Thirring precession is due to the rotation of the central mass. The total precession is calculated by combining the de Sitter precession with the Lense–Thirring precession.
Experimental confirmation
The geodetic effect was verified to a precision of better than 0.5% percent by Gravity Probe BGravity Probe B
Gravity Probe B is a satellite-based mission which launched on 20 April 2004 on a Delta II rocket. The spaceflight phase lasted until 2005; its aim was to measure spacetime curvature near Earth, and thereby the stress–energy tensor in and near Earth...
, an experiment which measures the tilting of the spin axis of gyroscope
Gyroscope
A gyroscope is a device for measuring or maintaining orientation, based on the principles of angular momentum. In essence, a mechanical gyroscope is a spinning wheel or disk whose axle is free to take any orientation...
s in orbit about the Earth. The first results were announced on April 14, 2007 at the meeting of the American Physical Society
American Physical Society
The American Physical Society is the world's second largest organization of physicists, behind the Deutsche Physikalische Gesellschaft. The Society publishes more than a dozen scientific journals, including the world renowned Physical Review and Physical Review Letters, and organizes more than 20...
.
Formulae
To derive the precession, assume the system is in a rotating Schwarzschild metricSchwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
. The nonrotating metric is

where c = 1.
We introduce a rotating coordinate system, with an angular velocity
 , such that a satellite in a circular orbit in the θ = π/2 plane remains at rest. This gives us
, such that a satellite in a circular orbit in the θ = π/2 plane remains at rest. This gives us
In this coordinate system, an observer at radial position r sees a vector positioned at r as rotating with angular frequency ω. This observer, however, sees a vector positioned at some other value of r as rotating at a different rate, due to relativistic time dilation. Transforming the Schwarzschild metric into the rotating frame, and assuming that
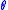 is a constant, we find
is a constant, we find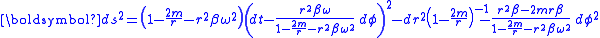
with
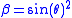 . For a body orbiting in the θ=π/2 plane, we will have β=1, and the body's world-line will maintain constant spatial coordinates for all time. Now, the metric is in the canonical form
. For a body orbiting in the θ=π/2 plane, we will have β=1, and the body's world-line will maintain constant spatial coordinates for all time. Now, the metric is in the canonical formCanonical form
Generally, in mathematics, a canonical form of an object is a standard way of presenting that object....
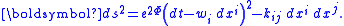
From this canonical form, we can easily determine the rotational rate of a gyroscope in proper time

where the last equality is true only for free falling observers for which
there is no acceleration, and thus
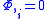 . This leads to
. This leads to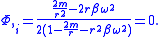
From this, we can distill
 ,
,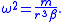
This is essentially Kepler's law of periods, which happens to be relativistically exact when expressed in terms of the time coordinate t of this particular rotating coordinate system. In the rotating frame, the satellite remains at rest, but an observer aboard the satellite sees the gyroscope's angular momentum vector precessing at the rate ω. This observer also sees the distant stars as rotating, but they rotate at a slightly different rate due to time dilation. Let τ be the gyroscope's proper time
Proper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
. Then
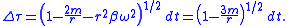
The −2m/r term is interpreted as the gravitational time dilation, while the additional −m/r is due to the rotation of this frame of reference. Let α' be the accumulated precession in the rotating frame. Since
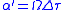 , the precession over the course of one orbit, relative to the distant stars, is given by:
, the precession over the course of one orbit, relative to the distant stars, is given by:
With a first-order Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
we find
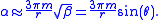
Thomas precession
One can attempt to break down the de Sitter precession into a kinematic effect called Thomas precessionThomas precession
In physics the Thomas precession, named after Llewellyn Thomas, is a special relativistic correction that applies to the spin of an elementary particle or the rotation of a macroscopic gyroscope and relates the angular velocity of the spin of a particle following a curvilinear orbit to the angular...
combined with a geometric effect caused by gravitationally curved spacetime. At least one author does describe it this way, but others state that "The Thomas precession comes into play for a gyroscope on the surface of the Earth ..., but not for a gyroscope in a freely moving satellite." An objection to the former interpretation is that the Thomas precession required has the wrong sign.
External links
- Gravity Probe B web site at NASA and Stanford University
- Precession in Curved Space "The Geodetic Effect"
- Geodetic Effect

