
Glicksberg's theorem
Encyclopedia
In the study of zero sum games
, Glicksberg's theorem (also Glicksberg's existence theorem) is a result that shows certain games have a minimax
value
.
If A and B are compact sets, and K is an upper semicontinuous or lower semicontinuous function on , then
, then
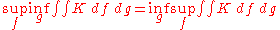
where f and g run over Borel probability measures on A and B.
The theorem is useful if f and g are interpreted as mixed strategies of two players in the context of a continuous game
. If the payoff function K is upper semicontinuous, then the game has a value.
The continuity condition may not be dropped: see example of a game with no value.
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, Glicksberg's theorem (also Glicksberg's existence theorem) is a result that shows certain games have a minimax
Minimax
Minimax is a decision rule used in decision theory, game theory, statistics and philosophy for minimizing the possible loss for a worst case scenario. Alternatively, it can be thought of as maximizing the minimum gain...
value
.
If A and B are compact sets, and K is an upper semicontinuous or lower semicontinuous function on
 , then
, then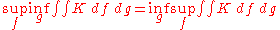
where f and g run over Borel probability measures on A and B.
The theorem is useful if f and g are interpreted as mixed strategies of two players in the context of a continuous game
Continuous game
A continuous game is a mathematical generalization, used in game theory. It extends the notion of a discrete game, where the players choose from a finite set of pure strategies...
. If the payoff function K is upper semicontinuous, then the game has a value.
The continuity condition may not be dropped: see example of a game with no value.

