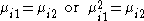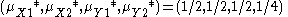Continuous game
Encyclopedia
A continuous game is a mathematical generalization, used in game theory
. It extends the notion of a discrete game, where the players choose from a finite set of pure strategies. The continuous game concepts allows games to include more general sets of pure strategies, which may be uncountably infinite.
In general, a game with uncountably infinite strategy sets will not necessarily have a Nash equilibrium
solution. If, however, the strategy sets are required to be compact
and the utility functions continuous
, then a Nash equilibrium will be guaranteed; this is by Glicksberg's generalization of the Kakutani fixed point theorem
. The class of continuous games is for this reason usually defined and studied as a subset of the larger class of infinite games (i.e. games with infinite strategy sets) in which the strategy sets are compact and the utility functions continuous.
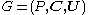 where
where
Let be a strategy profile of all players except for player
be a strategy profile of all players except for player 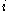 . As with discrete games, we can define a best response
. As with discrete games, we can define a best response
correspondence
for player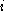 ,
,  .
. 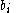 is a relation from the set of all probability distributions over opponent player profiles to a set of player
is a relation from the set of all probability distributions over opponent player profiles to a set of player  's strategies, such that each element of
's strategies, such that each element of
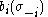
is a best response to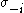 . Define
. Define
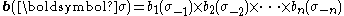 .
.
A strategy profile is a Nash equilibrium
is a Nash equilibrium
if and only if

The existence of a Nash equilibrium for any continuous game with continuous utility functions can been proven using Irving Glicksberg's generalization of the Kakutani fixed point theorem
. In general, there may not be a solution if we allow allow strategy spaces, 's which are not compact.
's which are not compact.
 can be expressed in the sum-of-products form:
can be expressed in the sum-of-products form:
A polynomial game is a separable game where each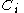 is a compact interval on
is a compact interval on  and each utility function can be written as a multivariate polynomial.
and each utility function can be written as a multivariate polynomial.
In general, mixed Nash equilibria of separable games are easier to compute than non-separable games as implied by the following theorem:
Whereas an equilibrium strategy for a non-separable game may require an uncountably infinite
support
, a separable game is guaranteed to have at least one Nash equilibrium with finitely supported mixed strategies.
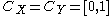 . Denote elements of
. Denote elements of  and
and 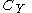 as
as  and
and 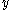 respectively. Define the utility functions
respectively. Define the utility functions 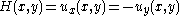 where
where
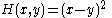 .
.
The pure strategy best response relations are:


 and
and 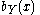 do not intersect, so there is
do not intersect, so there is
no pure strategy Nash equilibrium.
However, there should be a mixed strategy equilibrium. To find it, express the expected value, as a linear
as a linear
combination of the first and second moment
s of the probability distributions of X and Y:
(where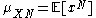 and similarly for Y).
and similarly for Y).
The constraints on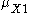 and
and 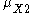 (with similar constraints for y,) are given by Hausdorff as:
(with similar constraints for y,) are given by Hausdorff as:
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
. It extends the notion of a discrete game, where the players choose from a finite set of pure strategies. The continuous game concepts allows games to include more general sets of pure strategies, which may be uncountably infinite.
In general, a game with uncountably infinite strategy sets will not necessarily have a Nash equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
solution. If, however, the strategy sets are required to be compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
and the utility functions continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, then a Nash equilibrium will be guaranteed; this is by Glicksberg's generalization of the Kakutani fixed point theorem
Kakutani fixed point theorem
In mathematical analysis, the Kakutani fixed-point theorem is a fixed-point theorem for set-valued functions. It provides sufficient conditions for a set-valued function defined on a convex, compact subset of a Euclidean space to have a fixed point, i.e. a point which is mapped to a set containing...
. The class of continuous games is for this reason usually defined and studied as a subset of the larger class of infinite games (i.e. games with infinite strategy sets) in which the strategy sets are compact and the utility functions continuous.
Formal definition
Define the n-player continuous game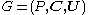 where
where
-
-
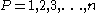 is the set of
is the set of  players,
players, -
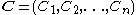 where each
where each  is a compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
is a compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
corresponding to the th player's set of pure strategies,
th player's set of pure strategies, -
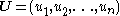 where
where 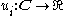 is the utility function of player
is the utility function of player 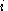
-
- We define
 to be the set of Borel probability measureProbability measureIn mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
to be the set of Borel probability measureProbability measureIn mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
s on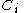 , giving us the mixed strategy space of player i.
, giving us the mixed strategy space of player i. - Define the strategy profile
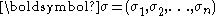 where
where 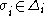
Let
 be a strategy profile of all players except for player
be a strategy profile of all players except for player 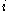 . As with discrete games, we can define a best response
. As with discrete games, we can define a best responseBest response
In game theory, the best response is the strategy which produces the most favorable outcome for a player, taking other players' strategies as given...
correspondence
Correspondence (mathematics)
In mathematics and mathematical economics, correspondence is a term with several related but not identical meanings.* In general mathematics, correspondence is an alternative term for a relation between two sets...
for player
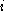 ,
,  .
. 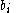 is a relation from the set of all probability distributions over opponent player profiles to a set of player
is a relation from the set of all probability distributions over opponent player profiles to a set of player  's strategies, such that each element of
's strategies, such that each element of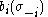
is a best response to
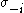 . Define
. Define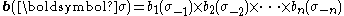 .
.A strategy profile
 is a Nash equilibrium
is a Nash equilibriumNash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
if and only if

The existence of a Nash equilibrium for any continuous game with continuous utility functions can been proven using Irving Glicksberg's generalization of the Kakutani fixed point theorem
Kakutani fixed point theorem
In mathematical analysis, the Kakutani fixed-point theorem is a fixed-point theorem for set-valued functions. It provides sufficient conditions for a set-valued function defined on a convex, compact subset of a Euclidean space to have a fixed point, i.e. a point which is mapped to a set containing...
. In general, there may not be a solution if we allow allow strategy spaces,
 's which are not compact.
's which are not compact.Separable games
A separable game is a continuous game where, for any i, the utility function can be expressed in the sum-of-products form:
can be expressed in the sum-of-products form:
-
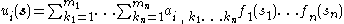 , where
, where  ,
, 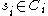 ,
,  , and the functions
, and the functions 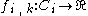 are continuous.
are continuous.
A polynomial game is a separable game where each
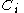 is a compact interval on
is a compact interval on  and each utility function can be written as a multivariate polynomial.
and each utility function can be written as a multivariate polynomial.In general, mixed Nash equilibria of separable games are easier to compute than non-separable games as implied by the following theorem:
- For any separable game there exists at least one Nash equilibrium where player i mixes at most
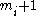 pure strategies.
pure strategies.
Whereas an equilibrium strategy for a non-separable game may require an uncountably infinite
Uncountable set
In mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.-Characterizations:There...
support
Support (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
, a separable game is guaranteed to have at least one Nash equilibrium with finitely supported mixed strategies.
A polynomial game
Consider a zero-sum 2-player game between players X and Y, with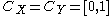 . Denote elements of
. Denote elements of  and
and 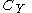 as
as  and
and 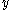 respectively. Define the utility functions
respectively. Define the utility functions 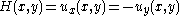 where
where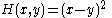 .
.The pure strategy best response relations are:


 and
and 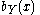 do not intersect, so there is
do not intersect, so there isno pure strategy Nash equilibrium.
However, there should be a mixed strategy equilibrium. To find it, express the expected value,
 as a linear
as a linearLinear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
combination of the first and second moment
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
s of the probability distributions of X and Y:
(where
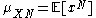 and similarly for Y).
and similarly for Y).The constraints on
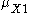 and
and 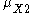 (with similar constraints for y,) are given by Hausdorff as:
(with similar constraints for y,) are given by Hausdorff as:-
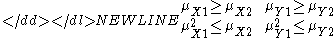
Each pair of constraints defines a compact convex subset in the plane. Since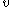 is linear, any extrema with respect to a player's first two moments will lie on the boundary of this subset. Player i's equilibrium strategy will lie on
is linear, any extrema with respect to a player's first two moments will lie on the boundary of this subset. Player i's equilibrium strategy will lie on
Note that the first equation only permits mixtures of 0 and 1 whereas the second equation only permits pure strategies. Moreover, if the best response at a certain point to player i lies on , it will lie on the whole line, so that both 0 and 1 are a best response.
, it will lie on the whole line, so that both 0 and 1 are a best response.  simply gives the pure strategy
simply gives the pure strategy 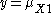 , so
, so  will never give both 0 and 1.
will never give both 0 and 1.
However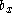 gives both 0 and 1 when y = 1/2.
gives both 0 and 1 when y = 1/2.
A Nash equilibrium exists when:
This determines one unique equilibrium where Player X plays a random mixture of 0 for 1/2 of the time and 1 the other 1/2 of the time. Player Y plays the pure strategy of 1/2. The value of the game is 1/4.
A rational pay-off function
Consider a zero-sum 2-player game between players X and Y, with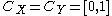 . Denote elements of
. Denote elements of 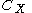 and
and 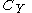 as
as  and
and 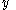 respectively. Define the utility functions
respectively. Define the utility functions 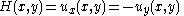 where
where
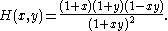
This game has no pure strategy Nash equilibrium. It can be shown that a unique mixed strategy Nash equilibrium exists with the following pair of probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
s:
The value of the game is .
.
Requiring a Cantor distribution
Consider a zero-sum 2-player game between players X and Y, with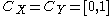 . Denote elements of
. Denote elements of 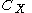 and
and 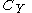 as
as 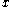 and
and 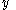 respectively. Define the utility functions
respectively. Define the utility functions 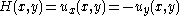 where
where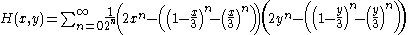 .
.
This game has a unique mixed strategy equilibrium where each player plays a mixed strategy with the cantor singular functionCantor functionIn mathematics, the Cantor function, named after Georg Cantor, is an example of a function that is continuous, but not absolutely continuous. It is also referred to as the Devil's staircase.-Definition:See figure...
as the cumulative distribution functionCumulative distribution functionIn probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
.
Further reading
- H. W. Kuhn and A. W. Tucker, eds. (1950). Contributions to the Theory of Games: Vol. II. Annals of Mathematics Studies 28. Princeton University Press. ISBN 0691079358.
-