Best response
Encyclopedia
In game theory
, the best response is the strategy
(or strategies) which produces the most favorable outcome
for a player, taking other players' strategies as given . The concept of a best response is central to John Nash's
best-known contribution, the Nash equilibrium
, the point at which each player in a game has selected the best response (or one of the best responses) to the other players' strategies .
Reaction correspondence
s, also known as best response correspondences, are used in the proof of the existence of mixed strategy Nash equilibria . Reaction correspondences are not "reaction functions" since functions
must only have one value per argument, and many reaction correspondences will be undefined, i.e. a vertical line, for some opponent strategy choice. One constructs a correspondence
, for each player from the set of opponent strategy profiles into the set of the player's strategies. So, for any given set of opponent's strategies 
, 
represents player i 's best responses to 
.
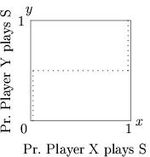Response correspondences for all 2x2 normal form game
s can be drawn with a line
for each player in a unit square
strategy space. Figures 1 to 3 graphs the best response correspondences for the stag hunt
game. The dotted line in Figure 1 shows the optimal
probability that player Y plays 'Stag' (in the y-axis), as a function of the probability that player X plays Stag (shown in the x-axis). In Figure 2 the dotted line shows the optimal probability that player X plays 'Stag' (shown in the x-axis), as a function of the probability that player Y plays Stag (shown in the y-axis). Note that Figure 2 plots the independent
and response variables in the opposite axes to those normally used, so that it may be superimposed onto the previous graph, to show the Nash equilibria
at the points where the two player's best responses agree in Figure 3.
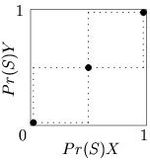
There are three distinctive reaction correspondence shapes, one for each of the three types of symmetric
2x2 games: coordination games, discoordination games and games with dominated strategies
(the trivial fourth case in which payoffs are always equal for both moves is not really a game theoretical problem). Any payoff symmetric 2x2 game will take one of these three forms.
and Battle of the sexes
are called coordination game
s. These games have reaction correspondences of the same shape as Figure 3, where there is one Nash equilibrium in the bottom left corner, another in the top right, and a mixing Nash somewhere along the diagonal between the other two.
Games such as the Game of chicken and Hawk-dove game in which players score highest when they choose opposite strategies, i.e., discoordinate, are called anti-coordination games. They have reaction correspondences (Figure 4) that cross in the opposite direction to coordination games, with three Nash equilibria, one in each of the top left and bottom right corners, where one player chooses one strategy, the other player chooses the opposite strategy. The third Nash equilibrium is a mixed strategy which lies along the diagonal from the bottom left to top right corners. If the players do not know which one of them is which, then the mixed Nash is an evolutionarily stable strategy
(ESS), as play is confined to the bottom left to top right diagonal line. Otherwise an uncorrelated asymmetry
is said to exist, and the corner Nash equilibria are ESSes.
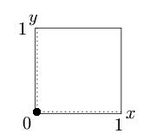Games with dominated
strategies have reaction correspondences which only cross at one point, which will be in either the bottom left, or top right corner in payoff symmetric 2x2 games. For instance, in the single-play Prisoner's dilemma
, the "Cooperate" move is not optimal for any probability of opponent Cooperation. Figure 5 shows the reaction correspondence for such a game, where the dimensions are "Probability play Cooperate", the Nash equilibrium is in the lower left corner where neither player plays Cooperate. If the dimensions were defined as "Probability play Defect", then both players best response curves would be 1 for all opponent strategy probabilities and the reaction correspondences would cross (and form a Nash equilibrium) at the top right corner.
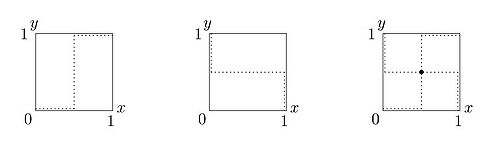
While there are only four possible types of payoff symmetric 2x2 games (of which one is trivial), the five different best response curves per player allow for a larger number of payoff asymmetric game types. Many of these are not truly different from each other. The dimensions may be redefined (exchange names of strategies 1 and 2) to produce symmetrical games which are logically identical.
game. In this game one player, the row player — graphed on the y dimension — wins if the players coordinate (both choose heads or both choose tails) while the other player, the column player — shown in the x-axis — wins if the players discoordinate. Player Y's reaction correspondence is that of a coordination game, while that of player X is a discoordination game. The only Nash equilibrium is the combination of mixed strategies where both players independently choose heads and tails with probability 0.5 each.
, best response dynamics represents a class of strategy updating rules, where players strategies in the next round are determined by their best responses to some subset of the population. Some examples include:
Importantly, in these models players only choose the best response on the next round that would give them the highest payoff on the next round. Players do not consider the effect that choosing a strategy on the next round would have on future play in the game. This constraint results in the dynamical rule often being called myopic best response.
Instead of best response correspondences, some models use smoothed best response functions. These functions are similar to the best response correspondence, except that the function does not "jump" from one pure strategy to another. The difference is illustrated in Figure 8, where black represents the best response correspondence and the other colors each represent different smoothed best response functions. In standard best response correspondences, even the slightest benefit to one action will result in the individual playing that action with probability 1. In smoothed best response as the difference between two actions decreases the individual's play approaches 50:50.
There are many functions that represent smoothed best response functions. The functions illustrated here are several variations on the following function:
where
represents the expected payoff of action 
, and 
is a parameter that determines the degree to which the function deviates from the true best response (a larger 
implies that the player is more likely to make 'mistakes').
There are several advantages to using smoothed best response, both theoretical and empirical. First, it is consistent with psychological experiments; when individuals are roughly indifferent between two actions they appear to choose more or less at random. Second, the play of individuals is uniquely determined in all cases, since the it is a function
and not a correspondence
. Finally, using smoothed best response with some learning rules (as in Fictitious play
) can result in players learning to play mixed strategy Nash equilibria .
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, the best response is the strategy
Strategy (game theory)
In game theory, a player's strategy in a game is a complete plan of action for whatever situation might arise; this fully determines the player's behaviour...
(or strategies) which produces the most favorable outcome
Outcome (Game theory)
In game theory, an outcome is a set of moves or strategies taken by the players, or their payoffs resulting from the actions or strategies taken by all players. The two are complementary in that, given knowledge of the set of strategies of all players, the final state of the game is known, as are...
for a player, taking other players' strategies as given . The concept of a best response is central to John Nash's
John Forbes Nash
John Forbes Nash, Jr. is an American mathematician whose works in game theory, differential geometry, and partial differential equations have provided insight into the forces that govern chance and events inside complex systems in daily life...
best-known contribution, the Nash equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
, the point at which each player in a game has selected the best response (or one of the best responses) to the other players' strategies .
Best response correspondence
Correspondence (mathematics)
In mathematics and mathematical economics, correspondence is a term with several related but not identical meanings.* In general mathematics, correspondence is an alternative term for a relation between two sets...
s, also known as best response correspondences, are used in the proof of the existence of mixed strategy Nash equilibria . Reaction correspondences are not "reaction functions" since functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
must only have one value per argument, and many reaction correspondences will be undefined, i.e. a vertical line, for some opponent strategy choice. One constructs a correspondence
, for each player from the set of opponent strategy profiles into the set of the player's strategies. So, for any given set of opponent's strategies , represents player i 's best responses to .Normal form game
In game theory, normal form is a way of describing a game. Unlike extensive form, normal-form representations are not graphical per se, but rather represent the game by way of a matrix. While this approach can be of greater use in identifying strictly dominated strategies and Nash equilibria, some...
s can be drawn with a line
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
for each player in a unit square
Unit square
In mathematics, a unit square is a square whose sides have length 1. Often, "the" unit square refers specifically to the square in the Cartesian plane with corners at , , , and .-In the real plane:...
strategy space. Figures 1 to 3 graphs the best response correspondences for the stag hunt
Stag hunt
In game theory, the stag hunt is a game which describes a conflict between safety and social cooperation. Other names for it or its variants include "assurance game", "coordination game", and "trust dilemma". Jean-Jacques Rousseau described a situation in which two individuals go out on a hunt. ...
game. The dotted line in Figure 1 shows the optimal
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
probability that player Y plays 'Stag' (in the y-axis), as a function of the probability that player X plays Stag (shown in the x-axis). In Figure 2 the dotted line shows the optimal probability that player X plays 'Stag' (shown in the x-axis), as a function of the probability that player Y plays Stag (shown in the y-axis). Note that Figure 2 plots the independent
Independent variable
The terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
and response variables in the opposite axes to those normally used, so that it may be superimposed onto the previous graph, to show the Nash equilibria
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
at the points where the two player's best responses agree in Figure 3.
There are three distinctive reaction correspondence shapes, one for each of the three types of symmetric
Symmetric game
In game theory, a symmetric game is a game where the payoffs for playing a particular strategy depend only on the other strategies employed, not on who is playing them. If one can change the identities of the players without changing the payoff to the strategies, then a game is symmetric. ...
2x2 games: coordination games, discoordination games and games with dominated strategies
(the trivial fourth case in which payoffs are always equal for both moves is not really a game theoretical problem). Any payoff symmetric 2x2 game will take one of these three forms.
Coordination games
Games in which players score highest when both players choose the same strategy, such as the Stag huntStag hunt
In game theory, the stag hunt is a game which describes a conflict between safety and social cooperation. Other names for it or its variants include "assurance game", "coordination game", and "trust dilemma". Jean-Jacques Rousseau described a situation in which two individuals go out on a hunt. ...
and Battle of the sexes
Battle of the sexes (game theory)
In game theory, battle of the sexes , also called Bach or Stravinsky, is a two-player coordination game. Imagine a couple that agreed to meet this evening, but cannot recall if they will be attending the opera or a football match. The husband would most of all like to go to the football game. The...
are called coordination game
Coordination game
In game theory, coordination games are a class of games with multiple pure strategy Nash equilibria in which players choose the same or corresponding strategies...
s. These games have reaction correspondences of the same shape as Figure 3, where there is one Nash equilibrium in the bottom left corner, another in the top right, and a mixing Nash somewhere along the diagonal between the other two.
Anti-coordination games
Evolutionarily stable strategy
In game theory and behavioural ecology, an evolutionarily stable strategy , which is sometimes also called an evolutionary stable strategy, is a strategy which, if adopted by a population of players, cannot be invaded by any alternative strategy that is initially rare. An ESS is an equilibrium...
(ESS), as play is confined to the bottom left to top right diagonal line. Otherwise an uncorrelated asymmetry
Uncorrelated asymmetry
In game theory an uncorrelated asymmetry is an arbitrary asymmetry in a game which is otherwise symmetrical. The name 'uncorrelated asymmetry' is due to John Maynard Smith who called payoff relevant asymmetries in games with similar roles for each player 'correlated asymmetries' .The explanation of...
is said to exist, and the corner Nash equilibria are ESSes.
Games with dominated strategies
Dominance (game theory)
In game theory, strategic dominance occurs when one strategy is better than another strategy for one player, no matter how that player's opponents may play...
strategies have reaction correspondences which only cross at one point, which will be in either the bottom left, or top right corner in payoff symmetric 2x2 games. For instance, in the single-play Prisoner's dilemma
Prisoner's dilemma
The prisoner’s dilemma is a canonical example of a game, analyzed in game theory that shows why two individuals might not cooperate, even if it appears that it is in their best interest to do so. It was originally framed by Merrill Flood and Melvin Dresher working at RAND in 1950. Albert W...
, the "Cooperate" move is not optimal for any probability of opponent Cooperation. Figure 5 shows the reaction correspondence for such a game, where the dimensions are "Probability play Cooperate", the Nash equilibrium is in the lower left corner where neither player plays Cooperate. If the dimensions were defined as "Probability play Defect", then both players best response curves would be 1 for all opponent strategy probabilities and the reaction correspondences would cross (and form a Nash equilibrium) at the top right corner.
Other (payoff asymmetric) games
A wider range of reaction correspondences shapes is possible in 2x2 games with payoff asymmetries. For each player there are five possible best response shapes, shown in Figure 6. From left to right these are: dominated strategy (always play 2), dominated strategy (always play 1), rising (play strategy 2 if probability that the other player plays 2 is above threshold), falling (play strategy 1 if probability that the other player plays 2 is above threshold), and indifferent (both strategies play equally well under all conditions).Matching pennies
One well-known game with payoff asymmetries is the matching penniesMatching pennies
Matching pennies is the name for a simple example game used in game theory. It is the two strategy equivalent of Rock, Paper, Scissors. Matching pennies is used primarily to illustrate the concept of mixed strategies and a mixed strategy Nash equilibrium....
game. In this game one player, the row player — graphed on the y dimension — wins if the players coordinate (both choose heads or both choose tails) while the other player, the column player — shown in the x-axis — wins if the players discoordinate. Player Y's reaction correspondence is that of a coordination game, while that of player X is a discoordination game. The only Nash equilibrium is the combination of mixed strategies where both players independently choose heads and tails with probability 0.5 each.
Best response dynamics
In evolutionary game theoryEvolutionary game theory
Evolutionary game theory is the application of Game Theory to evolving populations of lifeforms in biology. EGT is useful in this context by defining a framework of contests, strategies and analytics into which Darwinian competition can be modelled. It originated in 1973 with John Maynard Smith...
, best response dynamics represents a class of strategy updating rules, where players strategies in the next round are determined by their best responses to some subset of the population. Some examples include:
- In a large population model, players choose their next action probabilistically based on which strategies are best responses to the population as a whole.
- In a spatial model, players choose (in the next round) the action that is the best response to all of their neighbors .
Importantly, in these models players only choose the best response on the next round that would give them the highest payoff on the next round. Players do not consider the effect that choosing a strategy on the next round would have on future play in the game. This constraint results in the dynamical rule often being called myopic best response.
Smoothed best response
There are many functions that represent smoothed best response functions. The functions illustrated here are several variations on the following function:
where
represents the expected payoff of action , and is a parameter that determines the degree to which the function deviates from the true best response (a larger implies that the player is more likely to make 'mistakes').There are several advantages to using smoothed best response, both theoretical and empirical. First, it is consistent with psychological experiments; when individuals are roughly indifferent between two actions they appear to choose more or less at random. Second, the play of individuals is uniquely determined in all cases, since the it is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
and not a correspondence
Correspondence (mathematics)
In mathematics and mathematical economics, correspondence is a term with several related but not identical meanings.* In general mathematics, correspondence is an alternative term for a relation between two sets...
. Finally, using smoothed best response with some learning rules (as in Fictitious play
Fictitious play
In game theory, fictitious play is a learning rule first introduced by G.W. Brown . In it, each player presumes that the opponents are playing stationary strategies. At each round, each player thus best responds to the empirical frequency of play of his opponent...
) can result in players learning to play mixed strategy Nash equilibria .