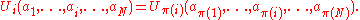Symmetric game
Encyclopedia
In game theory
, a symmetric game is a game where the payoffs for playing a particular strategy depend only on the other strategies employed, not on who is playing them. If one can change the identities of the players without changing the payoff to the strategies, then a game is symmetric. Symmetry can come in different varieties. Ordinally symmetric games are games that are symmetric with respect to the ordinal
structure of the payoffs. A game is quantitatively symmetric if and only if symmetric with respect to the exact payoffs.
Only 12 out the 144 ordinally distinct 2x2 games are symmetric. However, many of the commonly studied 2x2 games are at least ordinally symmetric. The standard representations of chicken, the Prisoner's Dilemma
, and the Stag hunt
are all symmetric games. Formally, in order for a 2x2 game to be symmetric, its payoff matrix must conform to the schema pictured to the right.
The requirements for a game to be ordinally symmetric are weaker, there it need only be the case that the ordinal ranking of the payoffs conform to the schema on the right.
. Cheng et al. (2004) show that every two-strategy symmetric game has a (not necessarily symmetric) pure strategy Nash equilibrium
.
which are purely informational and have no effect on payoffs (e.g. see Hawk-dove game).
where 
where 
is the payoff function for player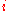 
and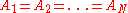 
is player 
's strategy set. Then the game is defined to be symmetric if for any permutation
,
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, a symmetric game is a game where the payoffs for playing a particular strategy depend only on the other strategies employed, not on who is playing them. If one can change the identities of the players without changing the payoff to the strategies, then a game is symmetric. Symmetry can come in different varieties. Ordinally symmetric games are games that are symmetric with respect to the ordinal
Ordinal
Ordinal may refer to:* Ordinal number , a word representing the rank of a number* Ordinal scale, ranking things that are not necessarily numbers* Ordinal indicator, the sign adjacent to a numeral denoting that it is an ordinal number...
structure of the payoffs. A game is quantitatively symmetric if and only if symmetric with respect to the exact payoffs.
Symmetry in 2x2 games
| E | F | |
|---|---|---|
| E | a, a | b, c |
| F | c, b | d, d |
Only 12 out the 144 ordinally distinct 2x2 games are symmetric. However, many of the commonly studied 2x2 games are at least ordinally symmetric. The standard representations of chicken, the Prisoner's Dilemma
Prisoner's dilemma
The prisoner’s dilemma is a canonical example of a game, analyzed in game theory that shows why two individuals might not cooperate, even if it appears that it is in their best interest to do so. It was originally framed by Merrill Flood and Melvin Dresher working at RAND in 1950. Albert W...
, and the Stag hunt
Stag hunt
In game theory, the stag hunt is a game which describes a conflict between safety and social cooperation. Other names for it or its variants include "assurance game", "coordination game", and "trust dilemma". Jean-Jacques Rousseau described a situation in which two individuals go out on a hunt. ...
are all symmetric games. Formally, in order for a 2x2 game to be symmetric, its payoff matrix must conform to the schema pictured to the right.
The requirements for a game to be ordinally symmetric are weaker, there it need only be the case that the ordinal ranking of the payoffs conform to the schema on the right.
Symmetry and equilibria
Nash (1951) shows that every symmetric game has a symmetric mixed strategy Nash equilibriumNash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
. Cheng et al. (2004) show that every two-strategy symmetric game has a (not necessarily symmetric) pure strategy Nash equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
.
Uncorrelated asymmetries: payoff neutral asymmetries
Symmetries here refer to symmetries in payoffs. Biologists often refer to asymmetries in payoffs between players in a game as correlated asymmetries. These are in contrast to uncorrelated asymmetriesUncorrelated asymmetry
In game theory an uncorrelated asymmetry is an arbitrary asymmetry in a game which is otherwise symmetrical. The name 'uncorrelated asymmetry' is due to John Maynard Smith who called payoff relevant asymmetries in games with similar roles for each player 'correlated asymmetries' .The explanation of...
which are purely informational and have no effect on payoffs (e.g. see Hawk-dove game).
The general case
Dasgupta and Maskin consider games where where is the payoff function for player and 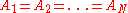is player 's strategy set. Then the game is defined to be symmetric if for any permutationPermutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
,