Evolutionary game theory
Encyclopedia
Evolutionary game theory (EGT) is the application of Game Theory
to evolving populations of lifeforms in biology
. EGT is useful in this context by defining a framework of contests, strategies and analytics into which Darwinian competition can be modelled. It originated in 1973 with John Maynard Smith
and George R. Price
's formalization of the way such contests can be analysed as “strategies” and the mathematical criteria which can be used to predict the resulting prevalence of such competing strategies. EGT differs from classical game theory by focusing more on the dynamics of strategy change as influenced not just by the quality of the various competing strategies, but on the effect the frequency of finding those various competing strategies in the population. Evolutionary game theory has proven itself to be of invaluable assistance in helping to explain many complex and challenging aspects of biology. It has been particularly helpful in establishing the basis of altruistic behaviours within the context of Darwinian process. Despite its origin and original purpose, evolutionary game theory has become of increasing interest to economists, sociologists, anthropologists, and philosophers.
The need for Evolutionary Game Theory in biology started with a problem. The problem was how to explain ritualized animal behaviour in a conflict situation. Why are animals so “gentlemanly or ladylike” in contests for resources? This was a problem that leading ethologists Niko Tinbergen and Konrad Lorenz
were trying to address. Tinbergen proposed that such behaviour exists for the benefit of the species. Maynard Smith couldn’t see this reasoning matched with Darwinian thought as he understood it, where selection occurs at an individual level and therefore defections to self-interest are rewarded while seeking the common good is not. Maynard Smith, an ex engineer and highly competent mathematician turned to Game theory to answer the question. The suggestion that Game Theory might solve the problem was made by George Price even though some unsuccessfully applied efforts by Richard Lewontin
at using game theory had failed. Maynard Smith’s way of applying this mathematics proved to be a far more realistic model, and came to be a major mathematical contribution in the field of theoretical biology.
was conceived by John Von Neumann
to mathematically help determine optimal strategies in situations where a competition between adversaries is taking place. A contest involves a number of players who all have a choice of moves for the game. Games can be a single round or repetitive. The approach a player has in making moves constitute the player “strategy”. Rules govern what will be the outcomes for the set of moves taken by the players and outcomes produce payoffs for the various players. Rules and resulting payoffs can be expressed as decision trees or in a payoff matrix. Classical game theory essentially requires that all the players make rational choices, making their strategic choice on a wholly rationally determined evaluation of probable outcomes. Therefore it is fundamental in Game Theory that each player must consider the strategic analysis that the players’ opponents are making, in determining that his own choice is appropriate.
does – it tests alternative strategies for the ability to survive and reproduce. In Biology
, strategies are genetically inherited traits that control an individuals action – and strategies are algorithmic – just like computer programs. The key point in the Evolutionary Game Theory model is that the success of a strategy is not just determined by how good the strategy is in itself, it is a question on how good the strategy is in the presence of other alternative strategies, and on the frequency that other strategies are employed within a competing population. It is also a question of how good a strategy plays against itself, because in the biological world a successful strategy will eventually dominate a population and competing individuals in it end up facing identical strategies to their own.
The object of the evolutionary game is to become more fit than competitors – to produce as many replicas of oneself as one can and the payoff is in units of Fitness (relative worth in being able to reproduce). It is always a multi-player game with a very large population of competitors. Rules describe the contest as in classical Game Theory but for evolutionary games rules include the element of replicator dynamics, in other words the general rules say exactly how the fitter players will spawn more replicas of themselves into the population and the less fit will be culled out of the player population (expressed in a Replicator Equation
). The replicator dynamics in essence models the heredity mechanism, but for simplicity leaves out mutation. Similarly, Evolutionary Game Theory only uses asexual reproduction for the sake of simplicity. Games are run repetitively with no terminating conditions. The results that are studied include the dynamics of changes in the population, the success/survival of strategies and any equilibrium states reached in a competing. Unlike classical Game Theory players do not choose their strategy or have the ability to change it, they are born with that strategy and their offspring will inherit that same identical strategy.
, it is a comprehensive model that encompasses the Darwinian process itself – including the central tenets of competition (the game) natural selection (replicator dynamics) and heredity - all within the overall model. Therefore it is a major vehicle to help understand and explain some of the most fundamental questions in biology including the issue of group selection
, sexual selection
, altruism
, parental care, co evolution, and ecological dynamics. Much of the progress in developing understanding in these diverse areas has been aided by Evolutionary Game Theory modelling and many of the counter intuitive situations in these areas have been explained and put on a firm mathematical footing by the use of these models.
The common methodology to study the evolutionary dynamics in games is through replicator equation
s. These replicator equations in the context of evolutionary biology shows the growth rate of the proportion of organisms using a certain strategy and that rate is equal to the difference between the average payoff of that strategy and the average payoff of the population as a whole. Continuous replicator equations assume infinite populations, continuous time, complete mixing
and that strategies breed true
. The attractor
s (stable fixed points) of the equations are equivalent with evolutionarily stable state
s. A strategy which can survive all "mutant" strategies is considered evolutionary stable. In the context of animal behavior, this usually means such strategies are programmed and heavily influenced by genetics
, thus making any player or organism's strategy determined by these biological factors.
Some representative games of Evolutionary Game Theory are Hawk/Dove, War of Attrition, Stag Hunt, Producer-Scrounger, Tragedy of the Commons, and Prisoners Dilemma. Some of the various strategies that apply in these games are Hawk, Dove, Bourgeois, Prober, Defector, Assessor, and Retaliator. Depending on the particular “Game” the various strategies vie against one another under the particular game rules, and the mathematics of the evolutionary game theory are used to determine the results and behaviors.
The strategy of the Hawk (a fighter strategy) is to first display aggression, then escalate into a fight till he either wins or else is injured.
The strategy of the Dove (fight avoider) is to first display aggression but if when faced with major escalation by an opponent will run for safety. If not faced with this level of escalation the Dove will attempt to share the resource.
Given that the resource is given the value V, the damage from losing a fight is given cost C:
The actual payoff however depends on the probability of meeting a Hawk or Dove, which in turn is a representation of the percentage of Hawks and Doves in the population when a particular contest takes place. But that population makeup in turn is determined by the results of all of the previous contests before the present contest- it is a continuous iterative process where the resultant population of the previous contest becomes the input population to the next contest.
If the cost of losing C is greater than the value of winning V (the normal situation in the natural world) the mathematics ends in an ESS – an evolutionary stable strategy situation having a mix of the two strategies where the population of Hawks is V/C. The population will progress back to this equilibrium point if any new Hawks or Doves make a temporary perturbation in the population.
The solution of the Hawk Dove Game explains why most animal contests involve only “ritual fighting behaviours” in contests rather than outright battles. The result does not at all depend on “good of the species” behaviours as suggested by Lorenz, but solely on the implication of actions of “selfish genes”.
There is a mutant strategy which can better that of Bluffer in the War of Attrition
Game. This is the Bourgeois strategy (Maynard Smith named the strategy Bourgeois, because with his background of communism he regarded it as “politically bourgeois” way to value ownership). Bourgeois uses an asymmetry of some sort to break the deadlock. In nature one such asymmetry is possession - which contestant has the prior possession of the resource. The strategy is to play a Hawk if in possession of the resource but to display then retreat if not in possession. This strategy requires greater cognitive capability than Hawk but Bourgeois is still a very prevalent strategy in many animal contests… some examples being Mantis Shrimp and Speckled Wood Butterfly contests.
Thus Evolutionary Game Theory explains a very wide range of rather mystifying behaviours in animals and in plant contests for many species with an illuminating clarity.
At first glance it may be surmised that the contestants of evolutionary games are the individuals present in each generation who directly participate in the game. On reflection however we see that individuals live only through one game cycle, and instead it is the strategies that really contest with one another over the full time span of these recursive games. So it is ultimately genes that play out a full contest – genes of STRATEGY (i.e. selfish genes). The contesting genes are not just present in an individual and his/her direct linage; they are also present to a relational degree in all of the individual’s kin. This can sometime profoundly affect the kinds of strategies that will survive, and nowhere is this more pertinent than in issues of cooperation and defection. Bill Hamilton, whose work defined kin selection, was involved in much of the groundbreaking mathematical work in this area and Hamilton treated many of these cases using game theoretic models. Kin related treatment of game contests help to explain many aspects of the behaviours of eusocial insects, the altruistic behaviour in parent/offspring interactions, mutual protection behaviours, and co-operative care of offspring. For such games Hamilton defined an extended form of fitness which is operative – Inclusive fitness
, which extends the fitness measure to include an individual’s offspring as well as any other “offspring equivalents” found in kin. Hamilton then went on beyond areas of kin relatedness to work with Robert Axelrod
to analyze games that involved co-operation under conditions not involving kin where reciprocal altruism
comes into play.
which carries out this approach by executing the simplest of algorithms.
in classical Game Theory, but with mathematically extended criteria. Nash Equilibrium is a game equilibrium where it is not rational for any player to deviate from the present strategy they are executing. As discussed, in Evolutionary game Theory contestants are NOT behaving with rational choice, nor do they have the ability to totally alter their strategy, aside from executing a very limited “mixed strategy”. An ESS is instead a state of game dynamics where, in a very large (or infinite) population of competitors, another mutant strategy cannot successfully enter the population to disturb the existing dynamic (which in itself is population mix dependent). This leads to a situation where to be a successful strategy having an ESS, the strategy must be both effective against competitors when it is rare - to enter the previous competing population, and also successful when later in high proportion in the population - to “defend itself”. This in turn necessarily means that the strategy needs to be successful when it contends with others exactly like itself.
ESS is NOT:
The ESS state can be solved for mathematically by exploring either the dynamics of population change to determine any ESS.... or alternatively by solving equations for the stable stationary point conditions which fundamentally define an ESS. For example, in the Hawk Dove Game we can look for whether there is a static population mix condition where the fitness of Doves will be exactly the same as fitness of Hawks (therefore both having equivalent growth rates - a "static point").
Let chance of meeting a Hawk=p so therefore the chance of meeting a dove is (1-p)
Let WHawk equal the Payoff for Hawk.....
WHawk=Payoff in the chance of meeting a Dove + Payoff in the chance of meeting a Hawk
Taking the PAYOFF MATRIX results and plugging them into the above equation:
Similarly for a Dove:
Equating the two fitnesses, Hawk and Dove
... and solving for p
so static Population percent:
ESS(percent Hawk)=V/C
Similarly using inequalities it can be shown that an additional Hawk or Dove “mutant” entering this ESS state generates a situation leading eventually to LESS fitness for their kind – both a true Nash and an ESS equilibrium.
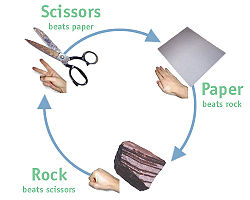An evolutionary game that actually turns out to be a children’s game is Rock Scissors Paper. The game is simple – rock bests scissors (blunts it), scissors bests paper (cuts it), and paper bests rock (wraps it up). Anyone who has ever played this simple game knows that it is not sensible to have any favoured play – your opponent will soon notice this and switch to the winning counter-play. The best strategy (a Nash equilibrium) is to play a mixed random game with any of the three plays taken a third of the time. This, in EGT terms, is a mixed strategy. But many lifeforms are incapable of mixed behaviour – they only exhibit one strategy (known as a “pure” strategy”). If the game is played only with the pure Rock, Scissor and Paper strategies the evolutionary game is dynamically unstable:
Rock mutants can enter an all scissor population, but then –
Paper mutants can take over an all Rock population, but then –
Scissor mutants can take over an all Paper population – and on and on….
This is easily seen on the game payoff matrix…
An Example in Nature - the Side-Blotched Lizard
The Side-Blotched Lizard (Uta stansburiana) is polymorphic with three morphs that each pursues a different mating strategy:
However the BlueThroats cannot overcome the more aggressive Orange Throats…
And on, and on… The overall situation corresponds to the exact form of the Rock, Scissors, Paper game and the dynamics is much the same. The populations for these lizards actually cycle on a six year basis. Once again EGT explains a very curious and otherwise inexplicable behaviour in the field of biology.
RPS and Ecology
Rock Scissors Paper is an evolutionary games that also helps to develop an understanding of Ecology
. In two strategy “pairwise” contests the outcome in most contests is that one strategy dominates the population and the dynamic reaches a static ESS point. This means in ecological terms, where it is species that compete with one another, that one particular species in these pairwise contests tends to dominate a particular ecological niche
. Most ecologies however are built up of multiple species (each successful in a separate niche), in intertwined or “intransitive” relationships, where each species benefits indirectly from a competition taking place between two other species, and where many species populations co-exist with a degree of cycling. These multi species ecologies have been modelled by game-theoretic analysis based on the Rock Scissors Paper game and results have been shown to produce dynamics that closely match with ecological systems in nature.
(RHP)” and shows that the effective cost to a competitor with higher RHP are not as great as for a competitor with a lower RHP. As a higher RHP individual is more desirable mate in producing potentially successful offspring, it is only logical that with sexual selection RHP should have evolved to be signalled in some way by the competing rivals, and for this to work this signally must be done HONESTLY. Amotz Zahavi
has developed this thinking in what is known as the Handicap Principle
, where superior competitors signal their superiority by a costly display. As higher RHP individuals can properly afford such a costly display this signalling is inherently honest, and can be taken as such by the signal receiver. Nowhere in nature is this better illustrated than in the magnificent and costly plumage of the male Peacock. The mathematical proof of the handicap principle was developed by Alan Grafen
using Evolutionary Game Theoretic modelling.
. In a paper by Carl Bergstrom
and Michael Lachmann, they successfully apply evolutionary game theory models to understand the division of benefits in mutualistic interactions between organisms. Darwinian assumptions about fitness are modeled using replicator dynamics to show that the organism evolving at a slower rate in a mutualistic relationship will gain a disproportionately high share of the benefits or payoffs. This application of EGT provided an interesting and perhaps unexpected twist on the Red Queen Hypothesis which concludes evolution favored faster rates of evolution.
analysing the behaviour of a system needs initially to be as simple as possible to aid in developing a base understanding the fundamentals, or “first order effects”, pertaining to what is being studied. With this understanding in place it is then appropriate to see if other, more subtle, parameters (second order effects) further impact the primary behaviours or shape additional behaviours in the system. Following Maynard Smith’s seminal work in EGT, the subject has had a number of very significant extensions which have shed more light on understanding evolutionary dynamics, particularly in the area of altruistic behaviors. Some of these key extensions to EGC are:
cannot be made. An important feature of all these sets of models under the umbrella of evolutionary game theory is repetition. If the games were not repeated, these EGT models would not be able to provide any insight into adaptive behaviors and strategies due to the dynamic nature of the mechanisms of evolution. Further, this biological application is meaningful for economics because it provides an understanding of the adjustments that occur between two equilibria (Samuelson 2002). While game theory provides a framework within which biologists can learn and understand organisms, the observation of evolution and how these strategies are applied helps economics illuminate processes. It is interesting to note however, that Maynard Smith himself never felt that the use of Evolutionary Game theory in the field of economics was quite relevant.
Sigmund, Karl; Game Theory – A Nontechnical Introduction, Dover Books, ISBN 0-486-29672-5
Dawkins, Richard; The Selfish Gene, Oxford University Press, ISBN 0-19-92114-4
Davis, Morton,; Game Theory – A Nontechnical Introduction, Dover Books, ISBN 0-486-29672-5
Maynard Smith, John; Evolution and the Theory of Games, Cambridge University Press, ISBN 0-521-28884-3
Dugatkin and Reeve; Game Theory and Animal Behavior, Oxford University Press, ISBN 0-19-513790-6
Nowak. Martin; Evolutionary Dynamics, Harvard University Press, ISBN 978-0-674-02338-3
Vincent and Brown; Evolutionary Game Theory, Natural Selection and Darwinian Dynamics,, Cambridge University Press, ISBN 0-521-84170-4
Hofbauer and Sigmund; Evolutionary Games and Population Dynamics, Cambridge University Press, ISBN 0-521-62570-X
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
to evolving populations of lifeforms in biology
Biology
Biology is a natural science concerned with the study of life and living organisms, including their structure, function, growth, origin, evolution, distribution, and taxonomy. Biology is a vast subject containing many subdivisions, topics, and disciplines...
. EGT is useful in this context by defining a framework of contests, strategies and analytics into which Darwinian competition can be modelled. It originated in 1973 with John Maynard Smith
John Maynard Smith
John Maynard Smith,His surname was Maynard Smith, not Smith, nor was it hyphenated. F.R.S. was a British theoretical evolutionary biologist and geneticist. Originally an aeronautical engineer during the Second World War, he took a second degree in genetics under the well-known biologist J.B.S....
and George R. Price
George R. Price
George Robert Price was an American population geneticist. Originally a physical chemist and later a science journalist, he moved to London in 1967, where he worked in theoretical biology at the Galton Laboratory, making three important contributions: first, rederiving W.D...
's formalization of the way such contests can be analysed as “strategies” and the mathematical criteria which can be used to predict the resulting prevalence of such competing strategies. EGT differs from classical game theory by focusing more on the dynamics of strategy change as influenced not just by the quality of the various competing strategies, but on the effect the frequency of finding those various competing strategies in the population. Evolutionary game theory has proven itself to be of invaluable assistance in helping to explain many complex and challenging aspects of biology. It has been particularly helpful in establishing the basis of altruistic behaviours within the context of Darwinian process. Despite its origin and original purpose, evolutionary game theory has become of increasing interest to economists, sociologists, anthropologists, and philosophers.
The Problem
"An ounce of algebra is worth a ton of verbal argument" J.B.S. Haldane(as quoted by John Maynard Smith)
The need for Evolutionary Game Theory in biology started with a problem. The problem was how to explain ritualized animal behaviour in a conflict situation. Why are animals so “gentlemanly or ladylike” in contests for resources? This was a problem that leading ethologists Niko Tinbergen and Konrad Lorenz
Konrad Lorenz
Konrad Zacharias Lorenz was an Austrian zoologist, ethologist, and ornithologist. He shared the 1973 Nobel Prize with Nikolaas Tinbergen and Karl von Frisch...
were trying to address. Tinbergen proposed that such behaviour exists for the benefit of the species. Maynard Smith couldn’t see this reasoning matched with Darwinian thought as he understood it, where selection occurs at an individual level and therefore defections to self-interest are rewarded while seeking the common good is not. Maynard Smith, an ex engineer and highly competent mathematician turned to Game theory to answer the question. The suggestion that Game Theory might solve the problem was made by George Price even though some unsuccessfully applied efforts by Richard Lewontin
Richard Lewontin
Richard Charles "Dick" Lewontin is an American evolutionary biologist, geneticist and social commentator. A leader in developing the mathematical basis of population genetics and evolutionary theory, he pioneered the notion of using techniques from molecular biology such as gel electrophoresis to...
at using game theory had failed. Maynard Smith’s way of applying this mathematics proved to be a far more realistic model, and came to be a major mathematical contribution in the field of theoretical biology.
Classical Game Theory
Game TheoryGame theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
was conceived by John Von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
to mathematically help determine optimal strategies in situations where a competition between adversaries is taking place. A contest involves a number of players who all have a choice of moves for the game. Games can be a single round or repetitive. The approach a player has in making moves constitute the player “strategy”. Rules govern what will be the outcomes for the set of moves taken by the players and outcomes produce payoffs for the various players. Rules and resulting payoffs can be expressed as decision trees or in a payoff matrix. Classical game theory essentially requires that all the players make rational choices, making their strategic choice on a wholly rationally determined evaluation of probable outcomes. Therefore it is fundamental in Game Theory that each player must consider the strategic analysis that the players’ opponents are making, in determining that his own choice is appropriate.
Adapting Game Theory to Evolutionary Games
On reflection Maynard Smith realised that in an evolutionary version of Game Theory it is not really a requirement that players be rational – it is only required that they have a strategy. The results of the game will test how good that strategy is. That is what EvolutionEvolution
Evolution is any change across successive generations in the heritable characteristics of biological populations. Evolutionary processes give rise to diversity at every level of biological organisation, including species, individual organisms and molecules such as DNA and proteins.Life on Earth...
does – it tests alternative strategies for the ability to survive and reproduce. In Biology
Biology
Biology is a natural science concerned with the study of life and living organisms, including their structure, function, growth, origin, evolution, distribution, and taxonomy. Biology is a vast subject containing many subdivisions, topics, and disciplines...
, strategies are genetically inherited traits that control an individuals action – and strategies are algorithmic – just like computer programs. The key point in the Evolutionary Game Theory model is that the success of a strategy is not just determined by how good the strategy is in itself, it is a question on how good the strategy is in the presence of other alternative strategies, and on the frequency that other strategies are employed within a competing population. It is also a question of how good a strategy plays against itself, because in the biological world a successful strategy will eventually dominate a population and competing individuals in it end up facing identical strategies to their own.
The object of the evolutionary game is to become more fit than competitors – to produce as many replicas of oneself as one can and the payoff is in units of Fitness (relative worth in being able to reproduce). It is always a multi-player game with a very large population of competitors. Rules describe the contest as in classical Game Theory but for evolutionary games rules include the element of replicator dynamics, in other words the general rules say exactly how the fitter players will spawn more replicas of themselves into the population and the less fit will be culled out of the player population (expressed in a Replicator Equation
Replicator equation
In mathematics, the replicator equation is a deterministic monotone non-linear and non-innovative game dynamic used in evolutionary game theory. The replicator equation differs from other equations used to model replication, such as the quasispecies equation, in that it allows the fitness landscape...
). The replicator dynamics in essence models the heredity mechanism, but for simplicity leaves out mutation. Similarly, Evolutionary Game Theory only uses asexual reproduction for the sake of simplicity. Games are run repetitively with no terminating conditions. The results that are studied include the dynamics of changes in the population, the success/survival of strategies and any equilibrium states reached in a competing. Unlike classical Game Theory players do not choose their strategy or have the ability to change it, they are born with that strategy and their offspring will inherit that same identical strategy.
Models
It is important to realise that EGT is not just a specialist mathematical treatment of animal contests to determine their dynamics and results, but in a manner similar to the field of Evolutionary AlgorithmsEvolutionary algorithm
In artificial intelligence, an evolutionary algorithm is a subset of evolutionary computation, a generic population-based metaheuristic optimization algorithm. An EA uses some mechanisms inspired by biological evolution: reproduction, mutation, recombination, and selection...
, it is a comprehensive model that encompasses the Darwinian process itself – including the central tenets of competition (the game) natural selection (replicator dynamics) and heredity - all within the overall model. Therefore it is a major vehicle to help understand and explain some of the most fundamental questions in biology including the issue of group selection
Group selection
In evolutionary biology, group selection refers to the idea that alleles can become fixed or spread in a population because of the benefits they bestow on groups, regardless of the alleles' effect on the fitness of individuals within that group....
, sexual selection
Sexual selection
Sexual selection, a concept introduced by Charles Darwin in his 1859 book On the Origin of Species, is a significant element of his theory of natural selection...
, altruism
Altruism
Altruism is a concern for the welfare of others. It is a traditional virtue in many cultures, and a core aspect of various religious traditions, though the concept of 'others' toward whom concern should be directed can vary among cultures and religions. Altruism is the opposite of...
, parental care, co evolution, and ecological dynamics. Much of the progress in developing understanding in these diverse areas has been aided by Evolutionary Game Theory modelling and many of the counter intuitive situations in these areas have been explained and put on a firm mathematical footing by the use of these models.
The common methodology to study the evolutionary dynamics in games is through replicator equation
Replicator equation
In mathematics, the replicator equation is a deterministic monotone non-linear and non-innovative game dynamic used in evolutionary game theory. The replicator equation differs from other equations used to model replication, such as the quasispecies equation, in that it allows the fitness landscape...
s. These replicator equations in the context of evolutionary biology shows the growth rate of the proportion of organisms using a certain strategy and that rate is equal to the difference between the average payoff of that strategy and the average payoff of the population as a whole. Continuous replicator equations assume infinite populations, continuous time, complete mixing
Complete mixing
In evolutionary game theory, complete mixing refers to an assumption about the type of interactions that occur between individual organisms. Interactions between individuals in a population attains complete mixing if and only if the probably individual x interacts with individual y is equal for...
and that strategies breed true
True breeding organism
A true breeding organism, sometimes also called a pure-bred, is an organism having certain biological traits which are passed on to all subsequent generations when bred with another true breeding organism for the same traits...
. The attractor
Attractor
An attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
s (stable fixed points) of the equations are equivalent with evolutionarily stable state
Evolutionarily stable state
"A population is said to be in an evolutionarily stable state if its genetic composition is restored by selection after a disturbance, provided the disturbance is not too large...
s. A strategy which can survive all "mutant" strategies is considered evolutionary stable. In the context of animal behavior, this usually means such strategies are programmed and heavily influenced by genetics
Genetics
Genetics , a discipline of biology, is the science of genes, heredity, and variation in living organisms....
, thus making any player or organism's strategy determined by these biological factors.
Games
In Game Theory various games are mathematical objects of different character –in rules, relative payoffs, and attendant mathematical behaviours. Each "game" represents different situations – in the kinds of problems that organisms have to deal with, and the possible strategies that they might adopt if they are to successfully survive and reproduce. To achieve a better feel for the challenges of these different situations, evolutionary games are often given rather colourful names and “cover stories” which quite effectively describe the general situation in which the particular game places its players … it all helps develop a feel for the mathematics of the game and the problems the players face.Some representative games of Evolutionary Game Theory are Hawk/Dove, War of Attrition, Stag Hunt, Producer-Scrounger, Tragedy of the Commons, and Prisoners Dilemma. Some of the various strategies that apply in these games are Hawk, Dove, Bourgeois, Prober, Defector, Assessor, and Retaliator. Depending on the particular “Game” the various strategies vie against one another under the particular game rules, and the mathematics of the evolutionary game theory are used to determine the results and behaviors.
Hawk Dove
The most classic game (and Maynard Smiths starting point) is the Hawk Dove game. The game was conceived to analyse the animal contest problem highlighted by Lorenz and Tinbergen. It is a contest over a sharable resource, say some food. The contestants can be either Hawk or Dove… this is not two separate species of bird; it is ONE species with two different types of strategy in the same species (two different morphs). The term Hawk Dove was coined by Maynard Smith because he did his work during the Vietnam War when political views fell into one of these two camps.The strategy of the Hawk (a fighter strategy) is to first display aggression, then escalate into a fight till he either wins or else is injured.
The strategy of the Dove (fight avoider) is to first display aggression but if when faced with major escalation by an opponent will run for safety. If not faced with this level of escalation the Dove will attempt to share the resource.
| meets Hawk | meets Dove | |
| if Hawk | V/2-C/2 | V |
| if Dove | 0 | V/2 |
Given that the resource is given the value V, the damage from losing a fight is given cost C:
- If a Hawk meets a Dove he gets the full resource V to himself
- If a Hawk meets a Hawk – half the time he wins, half the time he loses…so his average outcome is then V/2 minus C/2..
- If a Dove meets a Hawk he will back off and get nothing - 0
- If a Dove meets a Dove both share the resource and get V/2
The actual payoff however depends on the probability of meeting a Hawk or Dove, which in turn is a representation of the percentage of Hawks and Doves in the population when a particular contest takes place. But that population makeup in turn is determined by the results of all of the previous contests before the present contest- it is a continuous iterative process where the resultant population of the previous contest becomes the input population to the next contest.
If the cost of losing C is greater than the value of winning V (the normal situation in the natural world) the mathematics ends in an ESS – an evolutionary stable strategy situation having a mix of the two strategies where the population of Hawks is V/C. The population will progress back to this equilibrium point if any new Hawks or Doves make a temporary perturbation in the population.
The solution of the Hawk Dove Game explains why most animal contests involve only “ritual fighting behaviours” in contests rather than outright battles. The result does not at all depend on “good of the species” behaviours as suggested by Lorenz, but solely on the implication of actions of “selfish genes”.
The War of Attrition Game
In the Hawk Dove game the resource is sharable, which gives payoffs to both Doves meeting in a pairwise contest. In the case where the resource is not sharable but an alternative resource might be available by backing off and trying elsewhere, pure Hawk or Dove strategies become less effective. If an unshareable resource is combined with a high cost of losing a contest (injury or possible death) both Hawk and Dove payoffs are then further diminished. A safer strategy of display, bluffing and waiting to win, then becomes viable – a Bluffer strategy. The game then becomes one of accumulating costs, either the costs of displaying or costs of prolonged unresolved engagement. It’s effectively an auction; the winner is the contestant who will swallow the greater cost while the loser gets, for all his pains, the same cost as the winner but NO resource. The resulting evolutionary game theory mathematics leads to an optimal strategy of timed bluffing, where any player backs off with equal probability at any time in the contest - unguessable by his opponent. This is exactly what is observed in nature for contests in a number of species, for example between male dung flies contesting for mating sites. The timing of disengagement in these contests follows the exact mathematical curve derived from the evolutionary theory mathematics.There is a mutant strategy which can better that of Bluffer in the War of Attrition
War of attrition (game)
In game theory, the war of attrition is a model of aggression in which two contestants compete for a resource of value V by persisting while constantly accumulating costs over the time t that the contest lasts. The model was originally formulated by John Maynard Smith, a mixed evolutionary stable...
Game. This is the Bourgeois strategy (Maynard Smith named the strategy Bourgeois, because with his background of communism he regarded it as “politically bourgeois” way to value ownership). Bourgeois uses an asymmetry of some sort to break the deadlock. In nature one such asymmetry is possession - which contestant has the prior possession of the resource. The strategy is to play a Hawk if in possession of the resource but to display then retreat if not in possession. This strategy requires greater cognitive capability than Hawk but Bourgeois is still a very prevalent strategy in many animal contests… some examples being Mantis Shrimp and Speckled Wood Butterfly contests.
Thus Evolutionary Game Theory explains a very wide range of rather mystifying behaviours in animals and in plant contests for many species with an illuminating clarity.
Who is Playing the Game?
Inclusive fitness
In evolutionary biology and evolutionary psychology, the inclusive fitness of an organism is the sum of its classical fitness and the number of equivalents of its own offspring it can add to the population by supporting others...
, which extends the fitness measure to include an individual’s offspring as well as any other “offspring equivalents” found in kin. Hamilton then went on beyond areas of kin relatedness to work with Robert Axelrod
Robert Axelrod
Robert M. Axelrod is an American political scientist. He is Professor of Political Science and Public Policy at the University of Michigan where he has been since 1974. He is best known for his interdisciplinary work on the evolution of cooperation, which has been cited in numerous articles...
to analyze games that involved co-operation under conditions not involving kin where reciprocal altruism
Reciprocal altruism
In evolutionary biology, reciprocal altruism is a behaviour whereby an organism acts in a manner that temporarily reduces its fitness while increasing another organism's fitness, with the expectation that the other organism will act in a similar manner at a later time...
comes into play.
Prisoners Dilemma
One of the great difficulties of Darwinian Theory, and one recognised by Darwin himself was the problem of altruism. If the basis for selection is at the individual level, altruism makes no sense at all. But universal selection at the group level (for the good of the species, not the individual) fails to pass the test of the mathematics of game theory and is certainly not found to be the general case in nature. Yet in many social animals altruistic behaviour can be found. The solution to this paradox can be found in the application of Evolutionary Game Theory to the “Prisoners Dilemma” game - a game which tests the payoffs of cooperating or in defecting from cooperation. It is certainly the most studied game in all of mathematics. As with all games in Evolutionary Game Theory the analysis of Prisoners Dilemma is as a repetitive game. This repetitive nature affords competitors the possibility of retaliating for “bad behaviour” (defection) in previous rounds of the game. There is a multitude of strategies which have been tested by the mathematics of EGT and in computer simulations of contests and the conclusion is that the best competitive strategies are general cooperation with a reserved retaliatory response if necessary. The most famous and certainly one of the most successful of these strategies is Tit for TatTit for tat
Tit for tat is an English saying meaning "equivalent retaliation". It is also a highly effective strategy in game theory for the iterated prisoner's dilemma. It was first introduced by Anatol Rapoport in Robert Axelrod's two tournaments, held around 1980. An agent using this strategy will initially...
which carries out this approach by executing the simplest of algorithms.
| Tit for Tat Algorithm |
|---|
| EventBit=Trust; DO WHILE Contest=ON; IF Eventbit=Trust THEN Cooperate ELSE Defect; IF Opponent_Move=Cooperate THEN EventBit=Trust ELSE Eventbit=NOT(Trust); Loop; |
The ESS
The Evolutionary Stable Strategy (ESS) is perhaps the most widely known albeit most widely misunderstood concept in Evolutionary Game Theory. The ESS is basically akin to Nash EquilibriumNash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
in classical Game Theory, but with mathematically extended criteria. Nash Equilibrium is a game equilibrium where it is not rational for any player to deviate from the present strategy they are executing. As discussed, in Evolutionary game Theory contestants are NOT behaving with rational choice, nor do they have the ability to totally alter their strategy, aside from executing a very limited “mixed strategy”. An ESS is instead a state of game dynamics where, in a very large (or infinite) population of competitors, another mutant strategy cannot successfully enter the population to disturb the existing dynamic (which in itself is population mix dependent). This leads to a situation where to be a successful strategy having an ESS, the strategy must be both effective against competitors when it is rare - to enter the previous competing population, and also successful when later in high proportion in the population - to “defend itself”. This in turn necessarily means that the strategy needs to be successful when it contends with others exactly like itself.
ESS is NOT:
- An OPTIMAL strategy – an optimal strategy would maximize Fitness, and many ESS states are far below the maximum fitness achievable in a fitness landscape. (see Hawk Dove graph above as an example of this)
- A singular solution – often several ESS conditions can exist in a competitive situation. A particular contest might stabilize into any one of these possibilities, but later a major perturbation in conditions can move the solution into one of the alternative ESS states.
- Always present - It is also possible for there to be no ESS. An example evolutionary game with no ESS is the Rock-Scissors-Paper game found in a number of species (an example the side-blotched lizard (Uta stansburiana))
- An unbeatable strategy - The ESS strategy is not necessarily an unbeatable strategy, it is only an uninvadable one
The ESS state can be solved for mathematically by exploring either the dynamics of population change to determine any ESS.... or alternatively by solving equations for the stable stationary point conditions which fundamentally define an ESS. For example, in the Hawk Dove Game we can look for whether there is a static population mix condition where the fitness of Doves will be exactly the same as fitness of Hawks (therefore both having equivalent growth rates - a "static point").
Let chance of meeting a Hawk=p so therefore the chance of meeting a dove is (1-p)
Let WHawk equal the Payoff for Hawk.....
WHawk=Payoff in the chance of meeting a Dove + Payoff in the chance of meeting a Hawk
Taking the PAYOFF MATRIX results and plugging them into the above equation:
Similarly for a Dove:
Equating the two fitnesses, Hawk and Dove
... and solving for p
so static Population percent:ESS(percent Hawk)=V/C
Similarly using inequalities it can be shown that an additional Hawk or Dove “mutant” entering this ESS state generates a situation leading eventually to LESS fitness for their kind – both a true Nash and an ESS equilibrium.
Rock Scissors Paper Game
Rock mutants can enter an all scissor population, but then –
Paper mutants can take over an all Rock population, but then –
Scissor mutants can take over an all Paper population – and on and on….
This is easily seen on the game payoff matrix…
An Example in Nature - the Side-Blotched Lizard
Side-blotched lizard
Side-blotched lizards are lizards of the genus Uta. They are some of the most abundant and commonly observed lizards in the deserts of western North America. They commonly grow to six inches including the tail, with the males normally being the larger sex. Males often have bright throat colors....
The Side-Blotched Lizard (Uta stansburiana) is polymorphic with three morphs that each pursues a different mating strategy:
- The Orange throat is very aggressive and operates over a large territory - attempting to mate with numerous females within this larger area
- The unagressive Yellow Throat (called “sneakers”) mimic the markings/behavior of female lizards and sneakily slip into the Orange Throat's territory to mate with the females there (thereby overtaking the population), and
- The Blue Throat who mates with and carefully guards ONE female - making it impossible for the sneakers to succeed and therefore overtakes their place in a population…
However the BlueThroats cannot overcome the more aggressive Orange Throats…
And on, and on… The overall situation corresponds to the exact form of the Rock, Scissors, Paper game and the dynamics is much the same. The populations for these lizards actually cycle on a six year basis. Once again EGT explains a very curious and otherwise inexplicable behaviour in the field of biology.
RPS and Ecology
Rock Scissors Paper is an evolutionary games that also helps to develop an understanding of Ecology
Ecology
Ecology is the scientific study of the relations that living organisms have with respect to each other and their natural environment. Variables of interest to ecologists include the composition, distribution, amount , number, and changing states of organisms within and among ecosystems...
. In two strategy “pairwise” contests the outcome in most contests is that one strategy dominates the population and the dynamic reaches a static ESS point. This means in ecological terms, where it is species that compete with one another, that one particular species in these pairwise contests tends to dominate a particular ecological niche
Ecological niche
In ecology, a niche is a term describing the relational position of a species or population in its ecosystem to each other; e.g. a dolphin could potentially be in another ecological niche from one that travels in a different pod if the members of these pods utilize significantly different food...
. Most ecologies however are built up of multiple species (each successful in a separate niche), in intertwined or “intransitive” relationships, where each species benefits indirectly from a competition taking place between two other species, and where many species populations co-exist with a degree of cycling. These multi species ecologies have been modelled by game-theoretic analysis based on the Rock Scissors Paper game and results have been shown to produce dynamics that closely match with ecological systems in nature.
Signalling and the Handicap Principle
The problems of biological life are not at all unlike the problems that define economics – eating (akin to resource acquisition and management), survival (competitive strategy) and reproduction (investment, risk and return). Game theory was originally conceived as a mathematical analysis of economic processes and indeed this is why it has proven so useful in explaining so many biological behaviours. One important further refinement of the EGT model that has particular economic overtones rests on the analysis of COSTS. A simple model of cost assumes that all competitors suffer the same penalty imposed by the Game costs, but this is not the case. More successful players will be endowed with or will have accumulated a higher “wealth reserve” or “affordability” than less successful players. This wealth effect in Evolutionary Game Theory is represented mathematically by “resource holding potentialResource holding potential
In biology, resource holding potential is the ability of an animal to win an all-out fight if one were to take place.The term was coined by Geoff Parker to disambiguate physical fighting ability from the motivation to persevere in a fight . Originally the term used was 'Resource Holding Power',...
(RHP)” and shows that the effective cost to a competitor with higher RHP are not as great as for a competitor with a lower RHP. As a higher RHP individual is more desirable mate in producing potentially successful offspring, it is only logical that with sexual selection RHP should have evolved to be signalled in some way by the competing rivals, and for this to work this signally must be done HONESTLY. Amotz Zahavi
Amotz Zahavi
Amotz Zahavi is an Israeli evolutionary biologist, a Professor Emeritus at the Zoology Department of Tel Aviv University, and one of the founders of the Society for the Protection of Nature in Israel...
has developed this thinking in what is known as the Handicap Principle
Handicap principle
The handicap principle is a hypothesis originally proposed in 1975 by biologist Amotz Zahavi to explain how evolution may lead to "honest" or reliable signaling between animals who have an obvious motivation to bluff or deceive each other...
, where superior competitors signal their superiority by a costly display. As higher RHP individuals can properly afford such a costly display this signalling is inherently honest, and can be taken as such by the signal receiver. Nowhere in nature is this better illustrated than in the magnificent and costly plumage of the male Peacock. The mathematical proof of the handicap principle was developed by Alan Grafen
Alan Grafen
Alan Grafen is a Scottish ethologist and evolutionary biologist. He currently teaches and undertakes research at St John's College, Oxford. Along with regular contributions to scientific journals, Grafen is known publicly for his work as co-editor of the 2006 festschrift Richard Dawkins: How a...
using Evolutionary Game Theoretic modelling.
Co-Evolution
Evolutionary game theory models has thus been successfully applied to many areas of evolutionary biology with a recent development in the area of co-evolutionCo-evolution
In biology, coevolution is "the change of a biological object triggered by the change of a related object." Coevolution can occur at many biological levels: it can be as microscopic as correlated mutations between amino acids in a protein, or as macroscopic as covarying traits between different...
. In a paper by Carl Bergstrom
Carl Bergstrom
Carl T. Bergstrom is a theoretical and evolutionary biologist and a professor at the University of Washington , with a secondary appointment at the Santa Fe Institute. His work concerns the flow of information through biological and social networks and the ecology and evolution, including the...
and Michael Lachmann, they successfully apply evolutionary game theory models to understand the division of benefits in mutualistic interactions between organisms. Darwinian assumptions about fitness are modeled using replicator dynamics to show that the organism evolving at a slower rate in a mutualistic relationship will gain a disproportionately high share of the benefits or payoffs. This application of EGT provided an interesting and perhaps unexpected twist on the Red Queen Hypothesis which concludes evolution favored faster rates of evolution.
Extensions of the Evolutionary Game Theory Model
A mathematical modelMathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
analysing the behaviour of a system needs initially to be as simple as possible to aid in developing a base understanding the fundamentals, or “first order effects”, pertaining to what is being studied. With this understanding in place it is then appropriate to see if other, more subtle, parameters (second order effects) further impact the primary behaviours or shape additional behaviours in the system. Following Maynard Smith’s seminal work in EGT, the subject has had a number of very significant extensions which have shed more light on understanding evolutionary dynamics, particularly in the area of altruistic behaviors. Some of these key extensions to EGC are:
| Spatial Games | There are several very important influences attributable to geographic factors in the field of evolution – not least of which is gene flow Gene flow In population genetics, gene flow is the transfer of alleles of genes from one population to another.Migration into or out of a population may be responsible for a marked change in allele frequencies... and horizontal gene transfer Horizontal gene transfer Horizontal gene transfer , also lateral gene transfer , is any process in which an organism incorporates genetic material from another organism without being the offspring of that organism... . Spatial game models take geometry into effect by locating contestants in a lattice of cells over a two dimensional plane to represent this geographic element. In spatial games contests take place only with immediate neighbours. Winning strategies take over these immediate neighbourhoods and then go on to interact further with adjacent neighbourhoods. This model has been especially useful in showing how pockets of co-operators can invade and introduce altruism in the Prisoners Dilemma game, where for example Tit for Tat (TFT) is a Nash Equilibrium but NOT also an ESS. TFT cannot normally invade an all Defector population yet in spatial games this becomes possible. |
| Effects of having information | In conventional Game Theory Game theory Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others... the effect of Signalling (the acquisition of information) is of critical importance in outcomes. This can also be the case in EGT. Nowhere is this more important that in the area of studying Indirect Reciprocity in Prisoners Dilemma (where contests between the SAME paired individuals is NOT repetitive). This models the reality of most normal social interactions which are non-kin related. It has been shown that unless a probability measure of REPUTATION is available in Prisoners Dilemma only DIRECT reciprocity can be achievable. With this information INDIRECT reciprocity is also supported. |
| Finite populations | Many evolutionary games have been modelled in finite populations rather than infinite to see this effect this may have. Though in many cases this does not significantly alter game dynamics in others significant differences can and do occur, for example being in the prevalence of mixed strategies. |
Further Application
The successful application of game theory to evolution has brought further insights to human behavior. Whereas game theory traditionally assumes rational actors, in the real world this does not always describe human behavior. EGT has predicted behaviors in animals where strong assumptions of rationalityRationality
In philosophy, rationality is the exercise of reason. It is the manner in which people derive conclusions when considering things deliberately. It also refers to the conformity of one's beliefs with one's reasons for belief, or with one's actions with one's reasons for action...
cannot be made. An important feature of all these sets of models under the umbrella of evolutionary game theory is repetition. If the games were not repeated, these EGT models would not be able to provide any insight into adaptive behaviors and strategies due to the dynamic nature of the mechanisms of evolution. Further, this biological application is meaningful for economics because it provides an understanding of the adjustments that occur between two equilibria (Samuelson 2002). While game theory provides a framework within which biologists can learn and understand organisms, the observation of evolution and how these strategies are applied helps economics illuminate processes. It is interesting to note however, that Maynard Smith himself never felt that the use of Evolutionary Game theory in the field of economics was quite relevant.
See also
- Adaptive dynamics
- Behavioral ecologyBehavioral ecologyBehavioral ecology, or ethoecology, is the study of the ecological and evolutionary basis for animal behavior, and the roles of behavior in enabling an animal to adapt to its environment...
- Dynamical systems
- Evolution and the Theory of GamesEvolution and the Theory of GamesEvolution and the Theory of Games is a 1982 book by the British evolutionary biologist John Maynard Smith on evolutionary game theory. In it, Maynard Smith summarises work on evolutionary game theory that had developed in the 1970s, to which he made several important contributions...
(book) - Evolutionary stable strategy
- Gene-centered view of evolutionGene-centered view of evolutionThe gene-centered view of evolution, gene selection theory or selfish gene theory holds that evolution occurs through the differential survival of competing genes, increasing the frequency of those alleles whose phenotypic effects successfully promote their own propagation, with gene defined as...
- MemeticsMemeticsMemetics is a theory of mental content based on an analogy with Darwinian evolution, originating from Richard Dawkins' 1976 book The Selfish Gene. It purports to be an approach to evolutionary models of cultural information transfer. A meme, analogous to a gene, is essentially a "unit of...
- Evolutionary dynamicsEvolutionary dynamicsEvolutionary dynamics is the study of the mathematical principles according to which life has evolved and continues to evolve. In this area, Evolution has become a mathematical theory, and any idea of an evolutionary process or mechanism should be studied in the context of the mathematical...
Further Reading
For the Interested Layperson
Sigmund, Karl; Game Theory – A Nontechnical Introduction, Dover Books, ISBN 0-486-29672-5
Dawkins, Richard; The Selfish Gene, Oxford University Press, ISBN 0-19-92114-4
Davis, Morton,; Game Theory – A Nontechnical Introduction, Dover Books, ISBN 0-486-29672-5
For the Serious Reader
Maynard Smith, John; Evolution and the Theory of Games, Cambridge University Press, ISBN 0-521-28884-3
Dugatkin and Reeve; Game Theory and Animal Behavior, Oxford University Press, ISBN 0-19-513790-6
For the Mathematically Adept
Nowak. Martin; Evolutionary Dynamics, Harvard University Press, ISBN 978-0-674-02338-3
Vincent and Brown; Evolutionary Game Theory, Natural Selection and Darwinian Dynamics,, Cambridge University Press, ISBN 0-521-84170-4
Hofbauer and Sigmund; Evolutionary Games and Population Dynamics, Cambridge University Press, ISBN 0-521-62570-X