Coordination game
Encyclopedia
In game theory
, coordination games are a class of games with multiple pure strategy Nash equilibria
in which players choose the same or corresponding
strategies
. Coordination games are a formalization of the idea of a coordination problem, which is widespread in the social sciences
, including economics
, meaning situations in which all parties can realize mutual gains, but only by making mutually consistent decisions. A common application is the choice
of technological standards.
For a classic example of a coordination game, consider the 2-player, 2-strategy game, with the payoff matrix shown on the right (Fig. 1).
If this game is a coordination game, then the following inequalities in payoffs hold for player 1 (rows): A > B, D > C, and for player 2 (columns): a > c, d > b. In this game the strategy profiles {Left, Up} and {Right, Down} are pure Nash equilibria, marked in gray. This setup can be extended for more than two strategies, where strategies are usually sorted so that the Nash equilibria are in the diagonal from top left to bottom right, as well as game with more than two players.
In this case there are two pure Nash equilibria: either both swerve to the left, or both swerve to the right. In this example, it doesn't matter which side both players pick, as long as they both pick the same. Both solutions are Pareto efficient
. This is not true for all coordination games, as the pure coordination game in Fig. 3 shows. Pure (or common interest) coordination is the game where the players both prefer the same Nash equilibrium outcome, here both players prefer partying over both staying at home to watch TV. The {Party, Party} outcome Pareto dominates
the {Home, Home} outcome, just as both Pareto dominate the other two outcomes, {Party, Home} and {Home, Party}.
This is different in another type of coordination game commonly called battle of the sexes
(or conflicting interest coordination), as seen in Fig. 4. In this game both players prefer engaging in the same activity over going alone, but their preferences differ over which activity they should engage in. Player 1 prefers that they both party while player 2 prefers that they both stay at home.
Finally, the stag hunt
game in Fig. 5 shows a situation in which both players (hunters) can benefit if they cooperate (hunting a stag). However, cooperation might fail, because each hunter has an alternative which is safer because it does not require cooperation to succeed (hunting a hare). This example of the potential conflict between safety and social cooperation is originally due to Jean-Jacques Rousseau
.
. In the generic coordination game above, a mixed Nash equilibrium is given by probabilities p = (d-b)/(a+d-b-c) to play Up and 1-p to play Down for player 1, and q = (D-C)/(A+D-B-C) to play Left and 1-q to play Right for player 2. Since d > b and d-b < a+d-b-c, p is always between zero and one, so existence is assured (similarly for q).
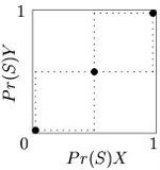
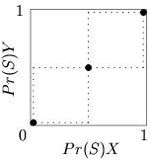
The reaction correspondences for 2×2 coordination games are shown in Fig. 6.
The pure Nash equilibria are the points in the bottom left and top right corners of the strategy space, while the mixed Nash equilibrium lies in the middle, at the intersection of the dashed lines.
Unlike the pure Nash equilibria, the mixed equilibrium is not an evolutionarily stable strategy
(ESS). The mixed Nash equilibrium is also Pareto dominated by the two pure Nash equilibria (since the players will fail to coordinate with non-zero probability), a quandary that led Robert Aumann
to propose the refinement of a correlated equilibrium
.
, may be more fair, or may be safer
. Sometimes these refinements conflict, which makes certain coordination games especially complicated and interesting (e.g. the Stag hunt
, in which {Stag,Stag} has higher payoffs, but {Hare,Hare} is safer).
, and in particular positive network externalities, the benefit reaped from being in the same network as other agents. Conversely, game theorists have modeled behavior under negative externalities where choosing the same action creates a cost rather than a benefit. The generic term for this class of game is anti-coordination game. The best-known example of a 2-player anti-coordination game is the game of Chicken
(also known as Hawk-Dove game). Using the payoff matrix in Figure 1, a game is an anti-coordination game if B > A and C > D for row-player 1 (with lowercase analogues for column-player 2). {Down, Left} and {Up, Right} are the two pure Nash equilibria. Chicken also requires that A > C, so a change from {Up, Left} to {Up, Right} improves player 2's payoff but reduces player 1's payoff, introducing conflict. This counters the standard coordination game setup, where all unilateral changes in a strategy lead to either mutual gain or mutual loss.
The concept of anti-coordination games has been extended to multi-player situation. A crowding game is defined as a game where each player's payoff is non-increasing over the number of other players choosing the same strategy (i.e., a game with negative network externalities). For instance, a driver could take U.S. Route 101 or Interstate 280
from San Francisco
to San Jose
. While 101 is shorter, 280 is considered more scenic, so drivers might have different preferences between the two independent of the traffic flow. But each additional car on either route will slightly increase the drive time on that route, so additional traffic creates negative network externalities, and even scenery-minded drivers might opt to take 101 if 280 becomes too crowded. A congestion game is a crowding game in networks. The minority game is a game where the only objective for all players is to be part of smaller of two groups. A well-known example of the minority game is the El Farol Bar problem
proposed by W. Brian Arthur
.
A hybrid form of coordination and anti-coordination is the discoordination game, where one player's incentive is to coordinate while the other player tries to avoid this. Discoordination games have no pure Nash equilibria. In Figure 1, choosing payoffs so that A > B, D < C, while a < b, c > d, creates a discoordination game. In each of the four possible states either player 1 or player 2 are better off by switching their strategy, so the only Nash equilirium is mixed. The canonical example of a discoordination game is the matching pennies
game.
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, coordination games are a class of games with multiple pure strategy Nash equilibria
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
in which players choose the same or corresponding
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
strategies
Strategy
Strategy, a word of military origin, refers to a plan of action designed to achieve a particular goal. In military usage strategy is distinct from tactics, which are concerned with the conduct of an engagement, while strategy is concerned with how different engagements are linked...
. Coordination games are a formalization of the idea of a coordination problem, which is widespread in the social sciences
Social sciences
Social science is the field of study concerned with society. "Social science" is commonly used as an umbrella term to refer to a plurality of fields outside of the natural sciences usually exclusive of the administrative or managerial sciences...
, including economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, meaning situations in which all parties can realize mutual gains, but only by making mutually consistent decisions. A common application is the choice
Decision making
Decision making can be regarded as the mental processes resulting in the selection of a course of action among several alternative scenarios. Every decision making process produces a final choice. The output can be an action or an opinion of choice.- Overview :Human performance in decision terms...
of technological standards.
For a classic example of a coordination game, consider the 2-player, 2-strategy game, with the payoff matrix shown on the right (Fig. 1).
If this game is a coordination game, then the following inequalities in payoffs hold for player 1 (rows): A > B, D > C, and for player 2 (columns): a > c, d > b. In this game the strategy profiles {Left, Up} and {Right, Down} are pure Nash equilibria, marked in gray. This setup can be extended for more than two strategies, where strategies are usually sorted so that the Nash equilibria are in the diagonal from top left to bottom right, as well as game with more than two players.
Examples
A typical case for a coordination game is choosing the side of the road upon which to drive, a social standard which can save lives if it is widely adhered to. In a simplified example, assume that two drivers meet on a narrow dirt road. Both have to swerve in order to avoid a head-on collision. If both execute the same swerving maneuver they will manage to pass each other, but if they choose differing maneuvers they will collide. In the payoff matrix in Fig. 2, successful passing is represented by a payoff of 10, and a collision by a payoff of 0.In this case there are two pure Nash equilibria: either both swerve to the left, or both swerve to the right. In this example, it doesn't matter which side both players pick, as long as they both pick the same. Both solutions are Pareto efficient
Pareto efficiency
Pareto efficiency, or Pareto optimality, is a concept in economics with applications in engineering and social sciences. The term is named after Vilfredo Pareto, an Italian economist who used the concept in his studies of economic efficiency and income distribution.Given an initial allocation of...
. This is not true for all coordination games, as the pure coordination game in Fig. 3 shows. Pure (or common interest) coordination is the game where the players both prefer the same Nash equilibrium outcome, here both players prefer partying over both staying at home to watch TV. The {Party, Party} outcome Pareto dominates
Pareto efficiency
Pareto efficiency, or Pareto optimality, is a concept in economics with applications in engineering and social sciences. The term is named after Vilfredo Pareto, an Italian economist who used the concept in his studies of economic efficiency and income distribution.Given an initial allocation of...
the {Home, Home} outcome, just as both Pareto dominate the other two outcomes, {Party, Home} and {Home, Party}.
This is different in another type of coordination game commonly called battle of the sexes
Battle of the sexes (game theory)
In game theory, battle of the sexes , also called Bach or Stravinsky, is a two-player coordination game. Imagine a couple that agreed to meet this evening, but cannot recall if they will be attending the opera or a football match. The husband would most of all like to go to the football game. The...
(or conflicting interest coordination), as seen in Fig. 4. In this game both players prefer engaging in the same activity over going alone, but their preferences differ over which activity they should engage in. Player 1 prefers that they both party while player 2 prefers that they both stay at home.
Finally, the stag hunt
Stag hunt
In game theory, the stag hunt is a game which describes a conflict between safety and social cooperation. Other names for it or its variants include "assurance game", "coordination game", and "trust dilemma". Jean-Jacques Rousseau described a situation in which two individuals go out on a hunt. ...
game in Fig. 5 shows a situation in which both players (hunters) can benefit if they cooperate (hunting a stag). However, cooperation might fail, because each hunter has an alternative which is safer because it does not require cooperation to succeed (hunting a hare). This example of the potential conflict between safety and social cooperation is originally due to Jean-Jacques Rousseau
Jean-Jacques Rousseau
Jean-Jacques Rousseau was a Genevan philosopher, writer, and composer of 18th-century Romanticism. His political philosophy influenced the French Revolution as well as the overall development of modern political, sociological and educational thought.His novel Émile: or, On Education is a treatise...
.
Mixed Nash equilibrium
Coordination games also have mixed strategy Nash equilibriaNash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
. In the generic coordination game above, a mixed Nash equilibrium is given by probabilities p = (d-b)/(a+d-b-c) to play Up and 1-p to play Down for player 1, and q = (D-C)/(A+D-B-C) to play Left and 1-q to play Right for player 2. Since d > b and d-b < a+d-b-c, p is always between zero and one, so existence is assured (similarly for q).
The reaction correspondences for 2×2 coordination games are shown in Fig. 6.
The pure Nash equilibria are the points in the bottom left and top right corners of the strategy space, while the mixed Nash equilibrium lies in the middle, at the intersection of the dashed lines.
Unlike the pure Nash equilibria, the mixed equilibrium is not an evolutionarily stable strategy
Evolutionarily stable strategy
In game theory and behavioural ecology, an evolutionarily stable strategy , which is sometimes also called an evolutionary stable strategy, is a strategy which, if adopted by a population of players, cannot be invaded by any alternative strategy that is initially rare. An ESS is an equilibrium...
(ESS). The mixed Nash equilibrium is also Pareto dominated by the two pure Nash equilibria (since the players will fail to coordinate with non-zero probability), a quandary that led Robert Aumann
Robert Aumann
Robert John Aumann is an Israeli-American mathematician and a member of the United States National Academy of Sciences. He is a professor at the Center for the Study of Rationality in the Hebrew University of Jerusalem in Israel...
to propose the refinement of a correlated equilibrium
Correlated equilibrium
In game theory, a correlated equilibrium is a solution concept that is more general than the well known Nash equilibrium. It was first discussed by mathematician Robert Aumann . The idea is that each player chooses his/her action according to his/her observation of the value of the same public...
.

Coordination and equilibrium selection
Games like the driving example above have illustrated the need for solution to coordination problems. Often we are confronted with circumstances where we must solve coordination problems without the ability to communicate with our partner. Many authors have suggested that particular equilibria are focal for one reason or another. For instance, some equilibria may give higher payoffs, be naturally more salientSalience (neuroscience)
The salience of an item – be it an object, a person, a pixel, etc – is the state or quality by which it stands out relative to its neighbours...
, may be more fair, or may be safer
Risk dominance
Risk dominance and payoff dominance are two related refinements of the Nash equilibrium solution concept in game theory, defined by John Harsanyi and Reinhard Selten. A Nash equilibrium is considered payoff dominant if it is Pareto superior to all other Nash equilibria in the game...
. Sometimes these refinements conflict, which makes certain coordination games especially complicated and interesting (e.g. the Stag hunt
Stag hunt
In game theory, the stag hunt is a game which describes a conflict between safety and social cooperation. Other names for it or its variants include "assurance game", "coordination game", and "trust dilemma". Jean-Jacques Rousseau described a situation in which two individuals go out on a hunt. ...
, in which {Stag,Stag} has higher payoffs, but {Hare,Hare} is safer).
Other games with externalities
Coordination games are closely linked to the economic concept of externalitiesExternality
In economics, an externality is a cost or benefit, not transmitted through prices, incurred by a party who did not agree to the action causing the cost or benefit...
, and in particular positive network externalities, the benefit reaped from being in the same network as other agents. Conversely, game theorists have modeled behavior under negative externalities where choosing the same action creates a cost rather than a benefit. The generic term for this class of game is anti-coordination game. The best-known example of a 2-player anti-coordination game is the game of Chicken
Chicken (game)
The game of chicken, also known as the hawk-dove or snowdrift game, is an influential model of conflict for two players in game theory...
(also known as Hawk-Dove game). Using the payoff matrix in Figure 1, a game is an anti-coordination game if B > A and C > D for row-player 1 (with lowercase analogues for column-player 2). {Down, Left} and {Up, Right} are the two pure Nash equilibria. Chicken also requires that A > C, so a change from {Up, Left} to {Up, Right} improves player 2's payoff but reduces player 1's payoff, introducing conflict. This counters the standard coordination game setup, where all unilateral changes in a strategy lead to either mutual gain or mutual loss.
The concept of anti-coordination games has been extended to multi-player situation. A crowding game is defined as a game where each player's payoff is non-increasing over the number of other players choosing the same strategy (i.e., a game with negative network externalities). For instance, a driver could take U.S. Route 101 or Interstate 280
Interstate 280 (California)
Interstate 280 is a 57-mile long north–south Interstate Highway in the San Francisco Bay Area of Northern California. It connects San Jose and San Francisco, running along just to the west of the cities of San Francisco Peninsula for most of its route.I-280 from its northern end at King...
from San Francisco
San Francisco, California
San Francisco , officially the City and County of San Francisco, is the financial, cultural, and transportation center of the San Francisco Bay Area, a region of 7.15 million people which includes San Jose and Oakland...
to San Jose
San Jose, California
San Jose is the third-largest city in California, the tenth-largest in the U.S., and the county seat of Santa Clara County which is located at the southern end of San Francisco Bay...
. While 101 is shorter, 280 is considered more scenic, so drivers might have different preferences between the two independent of the traffic flow. But each additional car on either route will slightly increase the drive time on that route, so additional traffic creates negative network externalities, and even scenery-minded drivers might opt to take 101 if 280 becomes too crowded. A congestion game is a crowding game in networks. The minority game is a game where the only objective for all players is to be part of smaller of two groups. A well-known example of the minority game is the El Farol Bar problem
El Farol bar problem
The El Farol bar problem is a problem in game theory. Based on a bar in Santa Fe, New Mexico, it was created in 1994 by W. Brian Arthur.The problem is as follows: There is a particular, finite population of people. Every Thursday night, all of these people want to go to the El Farol Bar. However,...
proposed by W. Brian Arthur
W. Brian Arthur
William Brian Arthur is an economist credited with influencing and describing the modern theory of increasing returns. He has lived and worked in Northern California for many years. He is an authority on economics in relation to complexity theory, technology and financial markets...
.
A hybrid form of coordination and anti-coordination is the discoordination game, where one player's incentive is to coordinate while the other player tries to avoid this. Discoordination games have no pure Nash equilibria. In Figure 1, choosing payoffs so that A > B, D < C, while a < b, c > d, creates a discoordination game. In each of the four possible states either player 1 or player 2 are better off by switching their strategy, so the only Nash equilirium is mixed. The canonical example of a discoordination game is the matching pennies
Matching pennies
Matching pennies is the name for a simple example game used in game theory. It is the two strategy equivalent of Rock, Paper, Scissors. Matching pennies is used primarily to illustrate the concept of mixed strategies and a mixed strategy Nash equilibrium....
game.
See also
- Consensus decision-makingConsensus decision-makingConsensus decision-making is a group decision making process that seeks the consent, not necessarily the agreement, of participants and the resolution of objections. Consensus is defined by Merriam-Webster as, first, general agreement, and second, group solidarity of belief or sentiment. It has its...
- Cooperative gameCooperative gameIn game theory, a cooperative game is a game where groups of players may enforce cooperative behaviour, hence the game is a competition between coalitions of players, rather than between individual players...
- Coordination failure (economics)Coordination failure (economics)In economics coordination failure is a concept that can explain recessions through the failure of firms and other price setters to coordinate. In an economic system with multiple equilibria, coordination failure occurs when a group of firms could achieve a more desirable equilibrium but fail to...
- Equilibrium selectionEquilibrium selectionEquilibrium selection is a concept from game theory which seeks to address reasons for players of a game to select a certain equilibrium over another...
- Non-cooperative gameNon-cooperative gameIn game theory, a non-cooperative game is one in which players make decisions independently. Thus, while they may be able to cooperate, any cooperation must be self-enforcing....
- Self-fulfilling prophecySelf-fulfilling prophecyA self-fulfilling prophecy is a prediction that directly or indirectly causes itself to become true, by the very terms of the prophecy itself, due to positive feedback between belief and behavior. Although examples of such prophecies can be found in literature as far back as ancient Greece and...
- Strategic complementsStrategic complementsIn economics and game theory, the decisions of two or more players are called strategic complements if they mutually reinforce one another, and they are called strategic substitutes if they mutually offset one another...
- SupermodularSupermodularIn mathematics, a functionf\colon R^k \to Ris supermodular iff + f \geq f + ffor all x, y \isin Rk, where x \vee y denotes the componentwise maximum and x \wedge y the componentwise minimum of x and y.If −f is supermodular then f is called submodular, and if the inequality is changed to an...
- Uniqueness or multiplicity of equilibrium

