
Normal form game
Encyclopedia
In game theory
, normal form is a way of describing a game. Unlike extensive form, normal-form representations are not graph
ical per se, but rather represent the game by way of a matrix
. While this approach can be of greater use in identifying strictly dominated strategies and Nash equilibria, some information is lost as compared to extensive-form representations. The normal-form representation of a game includes all perceptible and conceivable strategies
, and their corresponding payoffs, of each player.
In static games of complete
, perfect information
, a normal-form representation of a game is a specification of players' strategy spaces and payoff functions. A strategy space for a player is the set of all strategies available to that player, where a strategy is a complete plan of action for every stage of the game, regardless of whether that stage actually arises in play. A payoff function for a player is a mapping from the cross-product of players' strategy spaces to that player's set of payoffs (normally the set of real numbers, where the number represents a cardinal
or ordinal utility
—often cardinal in the normal-form representation) of a player, i.e. the payoff function of a player takes as its input a strategy profile (that is a specification of strategies for every player) and yields a representation of payoff as its output.
The matrix to the right is a normal-form representation of a game in which players move simultaneously (or at least do not observe the other player's move before making their own) and receive the payoffs as specified for the combinations of actions played. For example, if player 1 plays top and player 2 plays left, player 1 receives 4 and player 2 receives 3. In each cell, the first number represents the payoff to the row player (in this case player 1), and the second number represents the payoff to the column player (in this case player 2).
s (where the payoffs do not depend on which player chooses each action) are represented with only one payoff. This is the payoff for the row player. For example, the payoff matrices on the right and left below represent the same game.
The payoff matrix facilitates elimination of dominated strategies, and it is usually used to illustrate this concept. For example, in the prisoner's dilemma
(to the right), we can see that each prisoner can either "cooperate" or "defect". If exactly one prisoner defects, he gets off easily and the other prisoner is locked up for good. However, if they both defect, they will both be locked up for longer. One can determine that Cooperate is strictly dominated by Defect. One must compare the first numbers in each column, in this case 0 > −1 and −2 > −5. This shows that no matter what the column player chooses, the row player does better by choosing Defect. Similarly, one compares the second payoff in each row; again 0 > −1 and −2 > −5. This shows that no matter what row does, column does better by choosing Defect. This demonstrates the unique Nash equilibrium
of this game is (Defect, Defect).
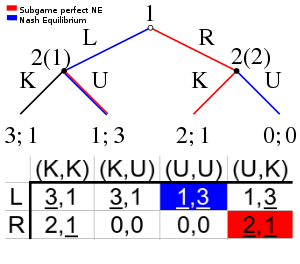
These matrices only represent games in which moves are simultaneous (or, more generally, information is imperfect
). The above matrix does not represent the game in which player 1 moves first, observed by player 2, and then player 2 moves, because it does not specify each of player 2's strategies in this case. In order to represent this sequential game
we must specify all of player 2's actions, even in contingencies that can never arise in the course of the game. In this game, player 2 has actions, as before, Left and Right. Unlike before he has four strategies, contingent on player 1's actions. The strategies are:
On the right is the normal-form representation of this game.
A pure strategy profile is an association of strategies to players, that is an m-tuple

such that

A payoff function is a function

whose intended interpretation is the award given to a single player at the outcome of the game. Accordingly, to completely specify a game, the payoff function has to be specified for each player in the player set P= {1, 2, ..., m}.
Definition: A game in normal form is a structure

where:

is a set of players,

is an m-tuple of pure strategy sets, one for each player, and

is an m-tuple of payoff functions.
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, normal form is a way of describing a game. Unlike extensive form, normal-form representations are not graph
Graph
Graph may refer to:* A graphic depicting the relationship between two or more variables used, for instance, in visualising scientific data.In mathematics:* Graph , is a set of vertices and edges....
ical per se, but rather represent the game by way of a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. While this approach can be of greater use in identifying strictly dominated strategies and Nash equilibria, some information is lost as compared to extensive-form representations. The normal-form representation of a game includes all perceptible and conceivable strategies
Strategy (game theory)
In game theory, a player's strategy in a game is a complete plan of action for whatever situation might arise; this fully determines the player's behaviour...
, and their corresponding payoffs, of each player.
In static games of complete
Complete information
Complete information is a term used in economics and game theory to describe an economic situation or game in which knowledge about other market participants or players is available to all participants. Every player knows the payoffs and strategies available to other players.Complete information...
, perfect information
Perfect information
In game theory, perfect information describes the situation when a player has available the same information to determine all of the possible games as would be available at the end of the game....
, a normal-form representation of a game is a specification of players' strategy spaces and payoff functions. A strategy space for a player is the set of all strategies available to that player, where a strategy is a complete plan of action for every stage of the game, regardless of whether that stage actually arises in play. A payoff function for a player is a mapping from the cross-product of players' strategy spaces to that player's set of payoffs (normally the set of real numbers, where the number represents a cardinal
Cardinal utility
In economics, cardinal utility refers to a property of mathematical indices that preserve preference orderings uniquely up to positive linear transformations...
or ordinal utility
Ordinal utility
Ordinal utility theory states that while the utility of a particular good or service cannot be measured using a numerical scale bearing economic meaning in and of itself, pairs of alternative bundles of goods can be ordered such that one is considered by an individual to be worse than, equal to,...
—often cardinal in the normal-form representation) of a player, i.e. the payoff function of a player takes as its input a strategy profile (that is a specification of strategies for every player) and yields a representation of payoff as its output.
An example
| Player 1 \ Player 2 | Player 2 chooses left | Player 2 chooses right |
|---|---|---|
| Player 1 chooses top | 4, 3 | −1, −1 |
| Player 1 chooses bottom | 0, 0 | 3, 4 |
The matrix to the right is a normal-form representation of a game in which players move simultaneously (or at least do not observe the other player's move before making their own) and receive the payoffs as specified for the combinations of actions played. For example, if player 1 plays top and player 2 plays left, player 1 receives 4 and player 2 receives 3. In each cell, the first number represents the payoff to the row player (in this case player 1), and the second number represents the payoff to the column player (in this case player 2).
Other representations
Often symmetric gameSymmetric game
In game theory, a symmetric game is a game where the payoffs for playing a particular strategy depend only on the other strategies employed, not on who is playing them. If one can change the identities of the players without changing the payoff to the strategies, then a game is symmetric. ...
s (where the payoffs do not depend on which player chooses each action) are represented with only one payoff. This is the payoff for the row player. For example, the payoff matrices on the right and left below represent the same game.
EWLINE
|
EWLINE
|
Dominated strategies
| Cooperate | Defect | |
|---|---|---|
| Cooperate | −1, −1 | −5, 0 |
| Defect | 0, −5 | −2, −2 |
The payoff matrix facilitates elimination of dominated strategies, and it is usually used to illustrate this concept. For example, in the prisoner's dilemma
Prisoner's dilemma
The prisoner’s dilemma is a canonical example of a game, analyzed in game theory that shows why two individuals might not cooperate, even if it appears that it is in their best interest to do so. It was originally framed by Merrill Flood and Melvin Dresher working at RAND in 1950. Albert W...
(to the right), we can see that each prisoner can either "cooperate" or "defect". If exactly one prisoner defects, he gets off easily and the other prisoner is locked up for good. However, if they both defect, they will both be locked up for longer. One can determine that Cooperate is strictly dominated by Defect. One must compare the first numbers in each column, in this case 0 > −1 and −2 > −5. This shows that no matter what the column player chooses, the row player does better by choosing Defect. Similarly, one compares the second payoff in each row; again 0 > −1 and −2 > −5. This shows that no matter what row does, column does better by choosing Defect. This demonstrates the unique Nash equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
of this game is (Defect, Defect).
Sequential games in normal form

| Left, Left | Left, Right | Right, Left | Right, Right | |
|---|---|---|---|---|
| Top | 4, 3 | 4, 3 | −1, −1 | −1, −1 |
| Bottom | 0, 0 | 3, 4 | 0, 0 | 3, 4 |
These matrices only represent games in which moves are simultaneous (or, more generally, information is imperfect
Perfect information
In game theory, perfect information describes the situation when a player has available the same information to determine all of the possible games as would be available at the end of the game....
). The above matrix does not represent the game in which player 1 moves first, observed by player 2, and then player 2 moves, because it does not specify each of player 2's strategies in this case. In order to represent this sequential game
Sequential game
In game theory, a sequential game is a game where one player chooses his action before the others choose theirs. Importantly, the later players must have some information of the first's choice, otherwise the difference in time would have no strategic effect...
we must specify all of player 2's actions, even in contingencies that can never arise in the course of the game. In this game, player 2 has actions, as before, Left and Right. Unlike before he has four strategies, contingent on player 1's actions. The strategies are:
- Left if player 1 plays Top and Left otherwise
- Left if player 1 plays Top and Right otherwise
- Right if player 1 plays Top and Left otherwise
- Right if player 1 plays Top and Right otherwise
On the right is the normal-form representation of this game.
General formulation
In order for a game to be in normal form, we are provided with the following data:- There is a finite set P of players, which we label {1, 2, ..., m}
- Each player k in P has a finite number of pure strategies
A pure strategy profile is an association of strategies to players, that is an m-tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...

such that

A payoff function is a function

whose intended interpretation is the award given to a single player at the outcome of the game. Accordingly, to completely specify a game, the payoff function has to be specified for each player in the player set P= {1, 2, ..., m}.
Definition: A game in normal form is a structure

where:

is a set of players,

is an m-tuple of pure strategy sets, one for each player, and

is an m-tuple of payoff functions.


