A golygon is any polygon

Polygon

In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...

 with all right angle

Right angle

In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...

s, whose sides are consecutive integer lengths. Golygons were invented and named by Lee Sallows

Lee Sallows

Lee Cecil Fletcher Sallows is a British electronics engineer known for his contributions to recreational mathematics. He is particularly noted as the inventor of golygons, self-enumerating sentences, and geomagic squares...

, and popularized by A. K. Dewdney in a 1990 Scientific American

Scientific American

Scientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...

 column (Smith). Variations on the definition of golygons involve allowing edges to cross, using sequences of edge lengths other than the consecutive integers, and considering turn angles other than 90°.

In any golygon, all horizontal edges have the same parity as each other, as do all vertical edges. Therefore, the number n of sides must allow the solution of the system of equations
It follows from this that n must be a multiple of 8.

The number of solutions to this system of equations may be computed efficiently using generating functions but finding the number of solutions that correspond to non-crossing golygons seems to be significantly more difficult.

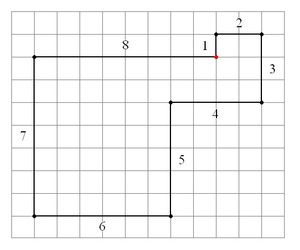
There is a unique eight-sided golygon (shown in the figure); it can tile

Tessellation

A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...

 the plane by 180-degree rotation using the Conway criterion.

External links

• Golygons at the On-Line Encyclopedia of Integer Sequences
  On-Line Encyclopedia of Integer Sequences
  The On-Line Encyclopedia of Integer Sequences , also cited simply as Sloane's, is an online database of integer sequences, created and maintained by N. J. A. Sloane, a researcher at AT&T Labs...