
Graded category
Encyclopedia
A graded category is a mathematical
concept.
If is a category
is a category
, then a
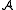 -graded category
-graded category
is a category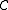 together with a functor
together with a functor
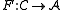 .
.
Monoid
s and group
s can be thought of as categories with a single element. A monoid-graded or group-graded category is therefore one in which to each morphism
is attached an element of a given monoid (resp. group), its grade. This must be compatible with composition
, in the sense that compositions have the product grade.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
concept.
If
 is a category
is a categoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, then a
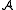 -graded category
-graded categoryis a category
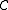 together with a functor
together with a functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
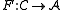 .
.Monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
s and group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s can be thought of as categories with a single element. A monoid-graded or group-graded category is therefore one in which to each morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
is attached an element of a given monoid (resp. group), its grade. This must be compatible with composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
, in the sense that compositions have the product grade.

