Gradient pattern analysis
Encyclopedia
Gradient pattern analysis (GPA) is a geometric computing method for characterizing symmetry breaking
of an ensemble of asymmetric vectors regularly distributed in a square lattice. Usually, the lattice of vectors represent the first-order gradient
of a scalar field, here an M x M square amplitude matrix
. An important property of the gradient representation is the following: A given M x M matrix where all amplitudes are different results in an M x M gradient lattice containing
asymmetric vectors. As each vector can be characterized by its norm and phase, variations in the 
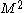amplitudes can modify the respective 
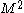gradient pattern.
The original concept of GPA was introduced by Rosa, Sharma and Valdivia in 1999. Usually GPA is applied for spatio-temporal pattern analysis in physics and environmental sciences operating on time-series and digital images.
criterion it is possible to characterize gradient asymmetries computing the so-called gradient asymmetry coefficient, that has been defined as:
,
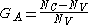where
is the total number of asymmetric vectors, 
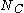is the number of Delaunay connections among them and the property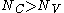 
is valid for any gradient square lattice.
As the asymmetry coefficient is very sensitive to small changes in the phase and modulus of each gradient vector, it can distinguish complex variability patterns even when they are very similar but consist of a very fine structural difference. Note that, unlike most of the statistical tools, the GPA does not rely on the statistical properties of the data but
depends solely on the local symmetry properties of the correspondent gradient pattern.
For a complex extended pattern (matrix of amplitudes of a spatio-temporal pattern) composed by locally asymmetric fluctuations,
is nonzero, defining different classes of irregular fluctuation patterns (1/f noise, chaotic, reactive-diffusive, etc.).
Besides
other measurements (called gradient moments) can be calculated from the gradient lattice.. Considering the sets of local norms and phases as discrete compact groups, spatially distributed in a square lattice, the gradient moments have the basic property of being globally invariant (for rotation and modulation).
The primary research on gradient lattices applied to characterize weak turbulence from X-ray images of solar active regions was developed in the Department of Astronomy at University of Maryland, College Park
, USA. A key line of research on GPA's algorithms and applications has been developed at Lab for Computing and Applied Mathematics (LAC) at National Institute for Space Research (INPE) in Brazil.
for KDE and this is the recommend platform to run it. GPA++ can be downloaded from Sourceforge.net.
Symmetry breaking
Symmetry breaking in physics describes a phenomenon where small fluctuations acting on a system which is crossing a critical point decide the system's fate, by determining which branch of a bifurcation is taken. To an outside observer unaware of the fluctuations , the choice will appear arbitrary...
of an ensemble of asymmetric vectors regularly distributed in a square lattice. Usually, the lattice of vectors represent the first-order gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of a scalar field, here an M x M square amplitude matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. An important property of the gradient representation is the following: A given M x M matrix where all amplitudes are different results in an M x M gradient lattice containing
asymmetric vectors. As each vector can be characterized by its norm and phase, variations in the 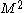amplitudes can modify the respective 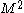gradient pattern.The original concept of GPA was introduced by Rosa, Sharma and Valdivia in 1999. Usually GPA is applied for spatio-temporal pattern analysis in physics and environmental sciences operating on time-series and digital images.
Calculation
By connecting all vectors using a Delaunay triangulationDelaunay triangulation
In mathematics and computational geometry, a Delaunay triangulation for a set P of points in a plane is a triangulation DT such that no point in P is inside the circumcircle of any triangle in DT. Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the...
criterion it is possible to characterize gradient asymmetries computing the so-called gradient asymmetry coefficient, that has been defined as:
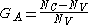,where
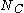is the total number of asymmetric vectors, is the number of Delaunay connections among them and the property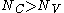 is valid for any gradient square lattice.
As the asymmetry coefficient is very sensitive to small changes in the phase and modulus of each gradient vector, it can distinguish complex variability patterns even when they are very similar but consist of a very fine structural difference. Note that, unlike most of the statistical tools, the GPA does not rely on the statistical properties of the data but
depends solely on the local symmetry properties of the correspondent gradient pattern.
For a complex extended pattern (matrix of amplitudes of a spatio-temporal pattern) composed by locally asymmetric fluctuations,
is nonzero, defining different classes of irregular fluctuation patterns (1/f noise, chaotic, reactive-diffusive, etc.).Besides
other measurements (called gradient moments) can be calculated from the gradient lattice.. Considering the sets of local norms and phases as discrete compact groups, spatially distributed in a square lattice, the gradient moments have the basic property of being globally invariant (for rotation and modulation).The primary research on gradient lattices applied to characterize weak turbulence from X-ray images of solar active regions was developed in the Department of Astronomy at University of Maryland, College Park
University of Maryland, College Park
The University of Maryland, College Park is a top-ranked public research university located in the city of College Park in Prince George's County, Maryland, just outside Washington, D.C...
, USA. A key line of research on GPA's algorithms and applications has been developed at Lab for Computing and Applied Mathematics (LAC) at National Institute for Space Research (INPE) in Brazil.
Relation to other methods
When GPA is conjugated with wavelet analysis, then the method is called Gradient spectral analysis (GSA), usually applied to short time series analysis.Code
Recently, a new implementation of the method was done. This was called GPA++, a C/C++ implementation of GPA. It is a Linux app that can run both under a Text based console or in a Graphical User Interface like KDE or GNOME. We developed it in Slackware 13for KDE and this is the recommend platform to run it. GPA++ can be downloaded from Sourceforge.net.