HMAC - AbsoluteAstronomy.com

Cryptography

Cryptography is the practice and study of techniques for secure communication in the presence of third parties...

, HMAC (Hash-based Message Authentication Code) is a specific construction for calculating a message authentication code

Message authentication code

In cryptography, a message authentication code is a short piece of information used to authenticate a message.A MAC algorithm, sometimes called a keyed hash function, accepts as input a secret key and an arbitrary-length message to be authenticated, and outputs a MAC...

(MAC) involving a cryptographic hash function

Cryptographic hash function

A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...

in combination with a secret key. As with any MAC, it may be used to simultaneously verify both the data integrity
Data integrity
Data Integrity in its broadest meaning refers to the trustworthiness of system resources over their entire life cycle. In more analytic terms, it is "the representational faithfulness of information to the true state of the object that the information represents, where representational faithfulness...

and the authenticity
Authentication
Authentication is the act of confirming the truth of an attribute of a datum or entity...

of a message. Any cryptographic hash function, such as MD5

MD5

The MD5 Message-Digest Algorithm is a widely used cryptographic hash function that produces a 128-bit hash value. Specified in RFC 1321, MD5 has been employed in a wide variety of security applications, and is also commonly used to check data integrity...

or SHA-1, may be used in the calculation of an HMAC; the resulting MAC algorithm is termed HMAC-MD5 or HMAC-SHA1 accordingly. The cryptographic strength of the HMAC depends upon the cryptographic strength of the underlying hash function, the size of its hash output length in bits, and on the size and quality of the cryptographic key.

An iterative hash function breaks up a message into blocks of a fixed size and iterates over them with a compression function. For example, MD5 and SHA-1 operate on 512-bit blocks. The size of the output of HMAC is the same as that of the underlying hash function (128 or 160 bits in the case of MD5 or SHA-1, respectively), although it can be truncated if desired.

The definition and analysis of the HMAC construction was first published in 1996 by Mihir Bellare

Mihir Bellare

Mihir Bellare is a cryptographer and professor at the University of California, San Diego. He has published several seminal papers in the field of cryptography , many coauthored with Phillip Rogaway. Bellare has published a number of papers in the field of Format-Preserving Encryption...

, Ran Canetti, and Hugo Krawczyk, who also wrote RFC 2104. This paper also defined a variant called NMAC that is rarely if ever used. FIPS

Federal Information Processing Standard

A Federal Information Processing Standard is a publicly announced standardization developed by the United States federal government for use in computer systems by all non-military government agencies and by government contractors, when properly invoked and tailored on a contract...

PUB 198 generalizes and standardizes the use of HMACs. HMAC-SHA-1 and HMAC-MD5 are used within the IPsec

IPsec

Internet Protocol Security is a protocol suite for securing Internet Protocol communications by authenticating and encrypting each IP packet of a communication session...

and TLS

Transport Layer Security

Transport Layer Security and its predecessor, Secure Sockets Layer , are cryptographic protocols that provide communication security over the Internet...

protocols.

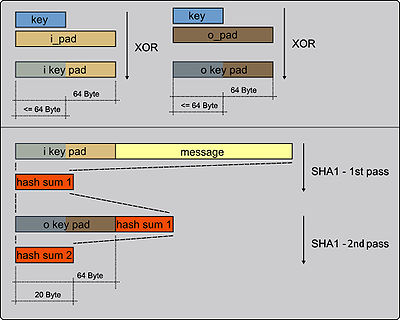
Definition (from RFC 2104)

Let:

H(·) be a cryptographic hash function
K be a secret key padded to the right with extra zeros to the input block size of the hash function, or the hash of the original key if it's longer than that block size
m be the message to be authenticated
∥ denote concatenation
Concatenation
In computer programming, string concatenation is the operation of joining two character strings end-to-end. For example, the strings "snow" and "ball" may be concatenated to give "snowball"...
⊕ denote exclusive or (XOR)
opad be the outer padding (0x5c5c5c…5c5c, one-block-long hexadecimal
Hexadecimal
In mathematics and computer science, hexadecimal is a positional numeral system with a radix, or base, of 16. It uses sixteen distinct symbols, most often the symbols 0–9 to represent values zero to nine, and A, B, C, D, E, F to represent values ten to fifteen...

constant) be the inner padding (0x363636…3636, one-block-long hexadecimal
Hexadecimal
In mathematics and computer science, hexadecimal is a positional numeral system with a radix, or base, of 16. It uses sixteen distinct symbols, most often the symbols 0–9 to represent values zero to nine, and A, B, C, D, E, F to represent values ten to fifteen...

constant)

Then HMAC(K,m) is mathematically defined by

HMAC(K,m) = H((K ⊕ opad) ∥ H((K ⊕ ipad) ∥ m)).

Implementation

The following pseudocode

Pseudocode

In computer science and numerical computation, pseudocode is a compact and informal high-level description of the operating principle of a computer program or other algorithm. It uses the structural conventions of a programming language, but is intended for human reading rather than machine reading...

demonstrates how HMAC may be implemented. Blocksize is 64 (bytes) when using one of the following hash functions: SHA-1, MD5, RIPEMD-128/160.

function hmac (key, message)
if (length(key) > blocksize) then
key = hash(key) // keys longer than blocksize are shortened
end if
if (length(key) < blocksize) then
key = key ∥ [0x00 * (blocksize - length(key))] // keys shorter than blocksize are zero-padded ('∥' is concatenation)
end if

o_key_pad = [0x5c * blocksize] ⊕ key // Where blocksize is that of the underlying hash function
i_key_pad = [0x36 * blocksize] ⊕ key // Where ⊕ is exclusive or (XOR)

return hash(o_key_pad ∥ hash(i_key_pad ∥ message)) // Where '∥' is concatenation
end function

Example usage

A business that suffers from attackers that place fraudulent Internet

Internet

The Internet is a global system of interconnected computer networks that use the standard Internet protocol suite to serve billions of users worldwide...

orders may insist that all its customers deposit a secret key with them. Along with an order, a customer must supply the order's HMAC digest, computed using the customer's symmetric key. The business, knowing the customer's symmetric key, can then verify that the order originated from the stated customer and has not been tampered with.

Design principles

The design of the HMAC specification was motivated by the existence of attacks on more trivial mechanisms for combining a key with a hash function. For example, one might assume the same security that HMAC provides could be achieved with MAC = H(key ∥ message). However, this method suffers from a serious flaw: with most hash functions, it is easy to append data to the message without knowing the key and obtain another valid MAC. The alternative, appending the key using MAC = H(message ∥ key), suffers from the problem that an attacker who can find a collision in the (unkeyed) hash function has a collision in the MAC. Using MAC = H(key ∥ message ∥ key) is better, however various security papers have suggested vulnerabilities with this approach, even when two different keys are used.

No known extensions attacks have been found against the current HMAC specification which is defined as H(key1 ∥ H(key2 ∥ message)) because the outer application of the hash function masks the intermediate result of the internal hash. The values of ipad and opad are not critical to the security of the algorithm, but were defined in such a way to have a large Hamming distance

Hamming distance

In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...

from each other and so the inner and outer keys will have fewer bits in common.

Security

The cryptographic strength of the HMAC depends upon the size of the secret key that is used. The most common attack against HMACs is brute force to uncover the secret key. HMACs are substantially less affected by collisions than their underlying hashing algorithms alone.

. Therefore, HMAC-MD5 does not suffer from the same weaknesses that have been found in MD5.

In 2006, Jongsung Kim, Alex Biryukov

Alex Biryukov

Alex Biryukov is a cryptographer, currently an assistant professor at the University of Luxembourg. His notable work includes the design of the stream cipher LEX, as well as the cryptanalysis of numerous cryptographic primitives. In 1998, he developed impossible differential cryptanalysis together...

, Bart Preneel

Bart Preneel

Bart Preneel is a Belgian cryptographer and cryptanalyst. He is a professor at Katholieke Universiteit Leuven, in the COSIC group, president of the International Association for Cryptologic Research, and project manager of ECRYPT....

, and Seokhie Hong showed how to distinguish HMAC with reduced versions of MD5 and SHA-1 or full versions of HAVAL

HAVAL

HAVAL is a cryptographic hash function. Unlike MD5, but like most modern cryptographic hash functions, HAVAL can produce hashes of different lengths. HAVAL can produce hashes in lengths of 128 bits, 160 bits, 192 bits, 224 bits, and 256 bits...

, MD4

MD4

The MD4 Message-Digest Algorithm is a cryptographic hash function developed by Ronald Rivest in 1990. The digest length is 128 bits. The algorithm has influenced later designs, such as the MD5, SHA-1 and RIPEMD algorithms....

, and SHA-0 from a random function

Random function

A random function is a function chosen at random from a finite family of functions. Typically, the family consists of the set of all maps from the domain to the codomain. Thus, a random function can be considered to map each input independently at random to any one of the possible outputs. Viewed...

or HMAC with a random function. Differential distinguishers allow an attacker to devise a forgery attack on HMAC. Furthermore, differential and rectangle distinguishers can lead to second-preimage attacks

Preimage attack

In cryptography, the preimage attack is a classification of attacks on hash functions for finding a message that has a specific hash value.There are two types of preimage attacks:...

. HMAC with the full version of MD4 can be forged

Forgery (Cryptography)

In a cryptographic digital signature or MAC system, digital signature forgery is the ability to create a pair consisting of a message m and a signature \sigma that is valid for m, where m has not been signed in the past by the legitimate signer...

with this knowledge. These attacks do not contradict the security proof of HMAC, but provide insight into HMAC based on existing cryptographic hash functions.

Examples of HMAC (MD5, SHA1, SHA256 )

Here are some empty HMAC values -
HMAC_MD5("", "") = 0x 74e6f7298a9c2d168935f58c001bad88
HMAC_SHA1("", "") = 0x fbdb1d1b18aa6c08324b7d64b71fb76370690e1d
HMAC_SHA256("", "") = 0x b613679a0814d9ec772f95d778c35fc5ff1697c493715653c6c712144292c5ad
Here are some non-empty HMAC values -
HMAC_MD5("key", "The quick brown fox jumps over the lazy dog") = 0x 80070713463e7749b90c2dc24911e275
HMAC_SHA1("key", "The quick brown fox jumps over the lazy dog") = 0x de7c9b85b8b78aa6bc8a7a36f70a90701c9db4d9
HMAC_SHA256("key", "The quick brown fox jumps over the lazy dog") = 0x f7bc83f430538424b13298e6aa6fb143ef4d59a14946175997479dbc2d1a3cd8

External links

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.