HNN extension
Encyclopedia
In mathematics
, the HNN extension is a basic construction of combinatorial group theory
.
Introduced in a 1949 paper Embedding Theorems for Groups by Graham Higman
, B. H. Neumann and Hanna Neumann
, it embeds a given group G into another group G' , in such a way that two given isomorphic subgroups of G are conjugate (through a given isomorphism) in G' .
be a group
with
presentation
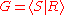, and let
be an isomorphism
between two subgroups
and 
of 
.
Let
be a new symbol not in 
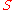, and define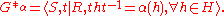
The group
is called the HNN extension of
relative to 
. The original group G is called the base group for the construction, while the subgroups 
and 
are the associated subgroups. The new generator 
is called the stable letter.
contains all the generators and relations from the presentation for
, there is a natural homomorphism, induced by the identification of generators, which takes 
to 
. Higman, Neumann and Neumann proved that this morphism is injective, that is, an embedding of 
into
. A consequence is that two isomorphic subgroups of a given group are always conjugate in some overgroup; the desire to show this was the original motivation for the construction.
as above, whenever in 
a product of the form
,
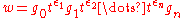where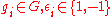
for 
,
satisfies
in 
then either n=0 and
in G or else for some 
one of the following holds:
Restated in contrapositive terms, Britton's Lemma says that if w is a product of the above form such that
then
in 
.
in algebraic topology
, the HNN extension is the construction required to understand the fundamental group of a topological space
X that has been 'glued back' on itself by a mapping f (see e.g. Surface bundle over the circle
). That is, HNN extensions stand in relation of that aspect of the fundamental group, as free products with amalgamation do with respect to the Seifert-van Kampen theorem for gluing spaces X and Y along a connected common subspace. Between the two constructions essentially any geometric gluing can be described, from the point of view of the fundamental group.
HNN-extensions play a key role in Higman's proof of the Higman embedding theorem
which states that every finitely generated recursively presented group can be homomorphically embedded in a finitely presented group. Most modern proofs of the Novikov-Boone theorem about the existence of a finitely presented group with algorithmically undecidable word problem
also substantially use HNN-extensions.
Both HNN-extensions and amalgamated free products are basic building blocks in the Bass–Serre theory of groups acting on trees.
The idea of HNN extension has been extended to other parts of abstract algebra
, including Lie algebra
theory.
, and as such are of central importance in Bass–Serre theory.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the HNN extension is a basic construction of combinatorial group theory
Combinatorial group theory
In mathematics, combinatorial group theory is the theory of free groups, and the concept of a presentation of a group by generators and relations...
.
Introduced in a 1949 paper Embedding Theorems for Groups by Graham Higman
Graham Higman
Graham Higman FRS was a leading British mathematician. He is known for his contributions to group theory....
, B. H. Neumann and Hanna Neumann
Hanna Neumann
Johanna Neumann was a German-born mathematician who worked on group theory.Johanna was born in Lankwitz, Steglitz-Zehlendorf, Germany. She attended Auguste-Viktoria-Schule and the University of Berlin and completed her studies in 1936 with distinctions in mathematics and physics. She began...
, it embeds a given group G into another group G' , in such a way that two given isomorphic subgroups of G are conjugate (through a given isomorphism) in G' .
Construction
Let be a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
with
presentation
Presentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
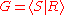, and let be an isomorphismGroup isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
between two subgroups
and of .Let
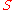be a new symbol not in , and define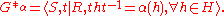The group
is called the HNN extension of relative to . The original group G is called the base group for the construction, while the subgroups and are the associated subgroups. The new generator is called the stable letter.Key properties
Since the presentation for contains all the generators and relations from the presentation for, there is a natural homomorphism, induced by the identification of generators, which takes to . Higman, Neumann and Neumann proved that this morphism is injective, that is, an embedding of into
. A consequence is that two isomorphic subgroups of a given group are always conjugate in some overgroup; the desire to show this was the original motivation for the construction.Britton's Lemma
A key property of HNN-extensions is a normal form theorem known as Britton's Lemma. It states that for a group as above, whenever in a product of the form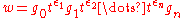,where
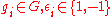for ,satisfies
in then either n=0 and
in G or else for some one of the following holds:
-
, -
.
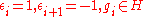Restated in contrapositive terms, Britton's Lemma says that if w is a product of the above form such that
- either n=0 and
in G, - or n>0 and the product w does not contain substrings of the form
, where 
and of the form 
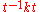where 
,
then
in .Consequences of Britton's Lemma
Most basic properties of HNN-extensions follow from Britton's Lemma. These consequences include the following facts:- The natural homomorphismGroup homomorphismIn mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
from G to
is injective, so that we can think of 
as containing G as a subgroupSubgroupIn group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
. - Every element of finite order in
is conjugateConjugacy classIn mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
to an element of G. - Every finite subgroup of
is conjugate to a finite subgroup of G. - If
and 
then 
contains a subgroup isomorphic to a free groupFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
of rank two.
Applications
In terms of the fundamental groupFundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, the HNN extension is the construction required to understand the fundamental group of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X that has been 'glued back' on itself by a mapping f (see e.g. Surface bundle over the circle
Surface bundle over the circle
In mathematics, a surface bundle over the circle is a fiber bundle with base space a circle, and with fiber space a surface. Therefore the total space has dimension 2 + 1 = 3. In general, fiber bundles over the circle are a special case of mapping tori....
). That is, HNN extensions stand in relation of that aspect of the fundamental group, as free products with amalgamation do with respect to the Seifert-van Kampen theorem for gluing spaces X and Y along a connected common subspace. Between the two constructions essentially any geometric gluing can be described, from the point of view of the fundamental group.
HNN-extensions play a key role in Higman's proof of the Higman embedding theorem
Higman's embedding theorem
In group theory, Higman's embedding theorem states that every finitely generated recursively presented group R can be embedded as a subgroup of some finitely presented group G...
which states that every finitely generated recursively presented group can be homomorphically embedded in a finitely presented group. Most modern proofs of the Novikov-Boone theorem about the existence of a finitely presented group with algorithmically undecidable word problem
Word problem for groups
In mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
also substantially use HNN-extensions.
Both HNN-extensions and amalgamated free products are basic building blocks in the Bass–Serre theory of groups acting on trees.
The idea of HNN extension has been extended to other parts of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, including Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
theory.
Generalizations
HNN extensions are elementary examples of fundamental groups of graphs of groupsGraph of groups
In geometric group theory, a graph of groups is an object consisting of a collection of groups indexed by the vertices and edges of a graph, together with a family of monomorphisms of the edge groups into the vertex groups....
, and as such are of central importance in Bass–Serre theory.