Hadamard's dynamical system
Encyclopedia
In physics
and mathematics
, the Hadamard dynamical system or Hadamard's billiards is a chaotic
dynamical system
, a type of dynamical billiards
. Introduced by Jacques Hadamard
in 1898, it is the first dynamical system to be proven chaotic
.
The system considers the motion of a free (friction
less) particle
on a surface of constant negative curvature
, the simplest compact Riemann surface
, which is the surface of genus two: a donut with two holes. Hadamard was able to show that every particle trajectory moves away from every other: that all trajectories have a positive Lyapunov exponent
.
Frank Steiner argues that Hadamard's study should be considered to be the first-ever examination of a chaotic dynamical system, and that Hadamard should be considered the first discoverer of chaos. He points out that the study was widely disseminated, and considers the impact of the ideas on the thinking of Albert Einstein
and Ernst Mach
.
The system is particularly important in that in 1963, Yakov Sinai, in studying Sinai's billiards as a model of the classical ensemble of a Boltzmann-Gibbs gas, was able to show that the motion of the atoms in the gas follow the trajectories in the Hadamard dynamical system.
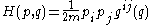
where m is the mass of the particle,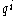
, 
are the coordinates on the manifold, 
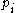are the conjugate momenta:
and
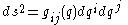
is the metric tensor
on the manifold. Because this is the free-particle Hamiltonian, the solution to the Hamilton–Jacobi equations of motion
are simply given by the geodesic
s on the manifold.
Hadamard was able to show that all geodesics are unstable, in that they all diverge exponentially from one-another, as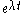
with positive Lyapunov exponent
with E the energy of a trajectory, and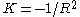
being the constant negative curvature of the surface.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Hadamard dynamical system or Hadamard's billiards is a chaotic
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
, a type of dynamical billiards
Dynamical billiards
A billiard is a dynamical system in which a particle alternates between motion in a straight line and specular reflections from a boundary. When the particle hits the boundary it reflects from it without loss of speed...
. Introduced by Jacques Hadamard
Jacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
in 1898, it is the first dynamical system to be proven chaotic
Randomness
Randomness has somewhat differing meanings as used in various fields. It also has common meanings which are connected to the notion of predictability of events....
.
The system considers the motion of a free (friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
less) particle
Subatomic particle
In physics or chemistry, subatomic particles are the smaller particles composing nucleons and atoms. There are two types of subatomic particles: elementary particles, which are not made of other particles, and composite particles...
on a surface of constant negative curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
, the simplest compact Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
, which is the surface of genus two: a donut with two holes. Hadamard was able to show that every particle trajectory moves away from every other: that all trajectories have a positive Lyapunov exponent
Lyapunov exponent
In mathematics the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories...
.
Frank Steiner argues that Hadamard's study should be considered to be the first-ever examination of a chaotic dynamical system, and that Hadamard should be considered the first discoverer of chaos. He points out that the study was widely disseminated, and considers the impact of the ideas on the thinking of Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
and Ernst Mach
Ernst Mach
Ernst Mach was an Austrian physicist and philosopher, noted for his contributions to physics such as the Mach number and the study of shock waves...
.
The system is particularly important in that in 1963, Yakov Sinai, in studying Sinai's billiards as a model of the classical ensemble of a Boltzmann-Gibbs gas, was able to show that the motion of the atoms in the gas follow the trajectories in the Hadamard dynamical system.
Exposition
The motion studied is that of a free particle sliding frictionlessly on the surface, namely, one having the HamiltonianHamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
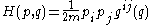
where m is the mass of the particle,
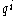, are the coordinates on the manifold, 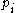are the conjugate momenta:and
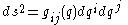
is the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
on the manifold. Because this is the free-particle Hamiltonian, the solution to the Hamilton–Jacobi equations of motion
Hamilton–Jacobi equation
In mathematics, the Hamilton–Jacobi equation is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations. In physics, the Hamilton–Jacobi equation is a reformulation of classical mechanics and, thus, equivalent to other formulations such as...
are simply given by the geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s on the manifold.
Hadamard was able to show that all geodesics are unstable, in that they all diverge exponentially from one-another, as
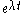with positive Lyapunov exponentLyapunov exponent
In mathematics the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories...
with E the energy of a trajectory, and
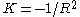being the constant negative curvature of the surface.