
Hall's universal group
Encyclopedia
In algebra
, Hall's universal group is
a countable locally finite group
, say U, which is uniquely
characterized by the following properties.
It was defined by Philip Hall
in 1959.
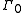 of order
of order 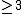 .
.
Denote by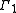 the group
the group 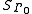
of permutation
s of elements of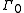 , by
, by
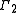 the group
the group
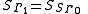
and so on. Since a group acts faithfully on itself by permutations
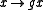
according to Cayley's theorem
, this gives a chain of monomorphisms
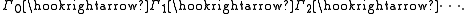
A direct limit
(that is, a union) of all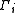
is Hall's universal group U.
Indeed, U then contains a symmetric group
of arbitrarily large order, and any
group admits a monomorphism to a group of permutations
, as explained above.
Let G be a finite group admitting two embeddings to U.
Since U is a direct limit and G is finite, the
images of these two embeddings belong to
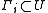 . The group
. The group
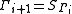 acts on
acts on 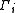
by permutations, and conjugates all possible embeddings
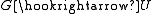 .
.
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, Hall's universal group is
a countable locally finite group
Locally finite group
In mathematics, in the field of group theory, a locally finite group is a type of group that can be studied in ways analogous to a finite group. Sylow subgroups, Carter subgroups, and abelian subgroups of locally finite groups have been studied....
, say U, which is uniquely
characterized by the following properties.
- Every finite group G admits a monomorphismMonomorphismIn the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
to U.
- All such monomorphisms are conjugate by inner automorphismInner automorphismIn abstract algebra an inner automorphism is a functionwhich, informally, involves a certain operation being applied, then another one performed, and then the initial operation being reversed...
s of U.
It was defined by Philip Hall
Philip Hall
Philip Hall FRS , was an English mathematician.His major work was on group theory, notably on finite groups and solvable groups.-Biography:...
in 1959.
Construction
Take any group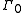 of order
of order 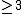 .
.Denote by
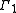 the group
the group 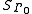
of permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s of elements of
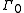 , by
, by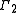 the group
the group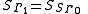
and so on. Since a group acts faithfully on itself by permutations
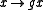
according to Cayley's theorem
Cayley's theorem
In group theory, Cayley's theorem, named in honor of Arthur Cayley, states that every group G is isomorphic to a subgroup of the symmetric group acting on G...
, this gives a chain of monomorphisms
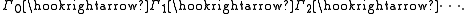
A direct limit
Direct limit
In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
(that is, a union) of all
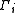
is Hall's universal group U.
Indeed, U then contains a symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
of arbitrarily large order, and any
group admits a monomorphism to a group of permutations
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
, as explained above.
Let G be a finite group admitting two embeddings to U.
Since U is a direct limit and G is finite, the
images of these two embeddings belong to
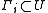 . The group
. The group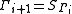 acts on
acts on 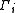
by permutations, and conjugates all possible embeddings
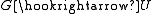 .
.

