Hardy–Littlewood zeta-function conjectures
Encyclopedia
In mathematics, the Hardy–Littlewood zeta-function conjectures, named after Godfrey Harold Hardy and John Edensor Littlewood
, are two conjectures concerning the distances between zeros and the density of zeros of the Riemann zeta function.
In 1914 Godfrey Harold Hardy
proved that the Riemann zeta function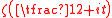
has infinitely many real zeros.
Let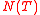
be the total number of real zeros, 
be the total number of zeros of odd order of the function 
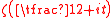, lying on the interval
.
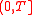Hardy and Littlewood claimed two conjectures. These conjectures – on the distance between real zeros of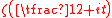
and on the density of zeros of 
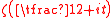on intervals 
for sufficiently great 
, 
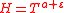and with as less as possible value of 
, where 
is an arbitrarily small number – open two new directions in the investigation of the Riemann zeta function.
1. For any
there exists such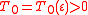 
that for 
and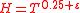 
the interval 
contains a zero of odd order of the function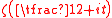 
.
2. For any
there exist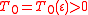 
and 
, such that for 
and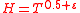 
the inequality 
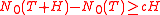is true.
In 1942 Atle Selberg
studied the problem 2 and proved that for any
there exists such 
and 
, such that for 
and 
the inequality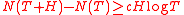 
is true.
In his turn, Selberg
claim his conjecture that it's possible to decrease the value of the exponent
for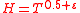 
which was proved forty-two years later by A.A. Karatsuba.
John Edensor Littlewood
John Edensor Littlewood was a British mathematician, best known for the results achieved in collaboration with G. H. Hardy.-Life:...
, are two conjectures concerning the distances between zeros and the density of zeros of the Riemann zeta function.
In 1914 Godfrey Harold Hardy
G. H. Hardy
Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
proved that the Riemann zeta function
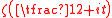has infinitely many real zeros.Let
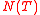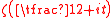be the total number of real zeros, be the total number of zeros of odd order of the function , lying on the interval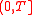.Hardy and Littlewood claimed two conjectures. These conjectures – on the distance between real zeros of
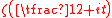and on the density of zeros of 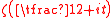on intervals for sufficiently great , 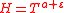and with as less as possible value of , where is an arbitrarily small number – open two new directions in the investigation of the Riemann zeta function.1. For any
there exists such 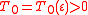that for and 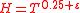the interval contains a zero of odd order of the function 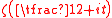.2. For any
there exist 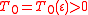and , such that for and 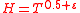the inequality 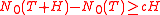is true.In 1942 Atle Selberg
Atle Selberg
Atle Selberg was a Norwegian mathematician known for his work in analytic number theory, and in the theory of automorphic forms, in particular bringing them into relation with spectral theory...
studied the problem 2 and proved that for any
there exists such and , such that for and the inequality 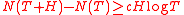is true.In his turn, Selberg
Atle Selberg
Atle Selberg was a Norwegian mathematician known for his work in analytic number theory, and in the theory of automorphic forms, in particular bringing them into relation with spectral theory...
claim his conjecture that it's possible to decrease the value of the exponent
for 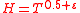which was proved forty-two years later by A.A. Karatsuba.