Harmonic progression (mathematics)
Encyclopedia
In mathematics
, a harmonic progression is a progression formed by taking the reciprocals of an arithmetic progression
. In other words, it is a sequence
of the form
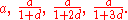
where −1/d is not a natural number
. Equivalently, a sequence is a harmonic progression when each term is the harmonic mean
of the neighboring terms.
Examples are
A, B, C, and D are such that D is the harmonic conjugate
of C with respect to A and B, then the distances from any one of these points to the three remaining points form harmonic progression. Specifically, each of the sequences
AC, AB, AD; BC, BA, BD; CA, CD, CB; and DA, DC, DB are harmonic progressions, where each of the distances is signed according to a fixed orientation of the line.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a harmonic progression is a progression formed by taking the reciprocals of an arithmetic progression
Arithmetic progression
In mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...
. In other words, it is a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of the form
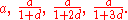
where −1/d is not a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
. Equivalently, a sequence is a harmonic progression when each term is the harmonic mean
Harmonic mean
In mathematics, the harmonic mean is one of several kinds of average. Typically, it is appropriate for situations when the average of rates is desired....
of the neighboring terms.
Examples are
- 12, 6, 4, 3,
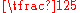, 2, … ,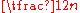 
- 10, 30, −30, −10, −6, −
, … , 
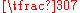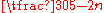
Use in geometry
If collinear pointsLine (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
A, B, C, and D are such that D is the harmonic conjugate
Projective harmonic conjugates
In projective geometry, the harmonic conjugate point of a triple of points on the real projective line is defined by the following construction due to Karl von Staudt:...
of C with respect to A and B, then the distances from any one of these points to the three remaining points form harmonic progression. Specifically, each of the sequences
AC, AB, AD; BC, BA, BD; CA, CD, CB; and DA, DC, DB are harmonic progressions, where each of the distances is signed according to a fixed orientation of the line.
See also
- Arithmetic progressionArithmetic progressionIn mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...
- Geometric progressionGeometric progressionIn mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression...
- Harmonic seriesHarmonic series (mathematics)In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...