Harnack's principle
Encyclopedia
In complex analysis
, Harnack's principle or Harnack's theorem is one of several closely related theorems about the convergence of sequences of harmonic function
s, that follow from Harnack's inequality
.
If the functions
, 
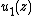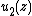, ... are harmonic in an open connected subset 
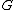of the complex plane
C, and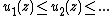
in every point of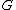
, then the limit
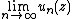
either is infinite in every point of the domain
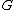or it is finite in every point of the domain, in both cases uniformly in each compact
subset of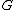
. In the latter case, the function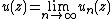
is harmonic in the set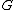
.
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, Harnack's principle or Harnack's theorem is one of several closely related theorems about the convergence of sequences of harmonic function
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
s, that follow from Harnack's inequality
Harnack's inequality
In mathematics, Harnack's inequality is an inequality relating the values of a positive harmonic function at two points, introduced by . and generalized Harnack's inequality to solutions of elliptic or parabolic partial differential equations. Perelman's solution of the Poincaré conjecture uses...
.
If the functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
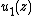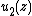, , ... are harmonic in an open connected subset 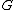of the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
C, and
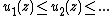
in every point of
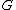, then the limitLimit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
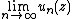
either is infinite in every point of the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
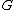or it is finite in every point of the domain, in both cases uniformly in each compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
subset of
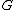. In the latter case, the function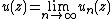is harmonic in the set
.
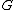