
Hasse norm theorem
Encyclopedia
In number theory
, the Hasse norm theorem states that if L/K is a cyclic extension of number fields, then if a nonzero element of K is a local norm everywhere, then it is a global norm.
Here to be a global norm means to be an element k of K such that there is an element l of L with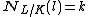 ; in other words k is a relative norm of some element of the extension field L. To be a local norm means that for some prime p of K and some prime P of L lying over K, then k is a norm from LP; here the "prime" p can be an archimedean valuation, and the theorem is a statement about completions in all valuations, archimedean and non-archimedean.
; in other words k is a relative norm of some element of the extension field L. To be a local norm means that for some prime p of K and some prime P of L lying over K, then k is a norm from LP; here the "prime" p can be an archimedean valuation, and the theorem is a statement about completions in all valuations, archimedean and non-archimedean.
The theorem is no longer true in general if the extension is abelian but not cyclic. A counter-example is given by the field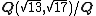 where every rational square is a local norm everywhere but
where every rational square is a local norm everywhere but 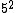 is not a global norm.
is not a global norm.
This is an example of a theorem stating a local-global principle, and is due to Helmut Hasse
.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the Hasse norm theorem states that if L/K is a cyclic extension of number fields, then if a nonzero element of K is a local norm everywhere, then it is a global norm.
Here to be a global norm means to be an element k of K such that there is an element l of L with
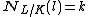 ; in other words k is a relative norm of some element of the extension field L. To be a local norm means that for some prime p of K and some prime P of L lying over K, then k is a norm from LP; here the "prime" p can be an archimedean valuation, and the theorem is a statement about completions in all valuations, archimedean and non-archimedean.
; in other words k is a relative norm of some element of the extension field L. To be a local norm means that for some prime p of K and some prime P of L lying over K, then k is a norm from LP; here the "prime" p can be an archimedean valuation, and the theorem is a statement about completions in all valuations, archimedean and non-archimedean.The theorem is no longer true in general if the extension is abelian but not cyclic. A counter-example is given by the field
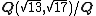 where every rational square is a local norm everywhere but
where every rational square is a local norm everywhere but 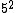 is not a global norm.
is not a global norm.This is an example of a theorem stating a local-global principle, and is due to Helmut Hasse
Helmut Hasse
Helmut Hasse was a German mathematician working in algebraic number theory, known for fundamental contributions to class field theory, the application of p-adic numbers to local classfield theory and diophantine geometry , and to local zeta functions.-Life:He was born in Kassel, and died in...
.

