Hausdorff density
Encyclopedia
In measure theory, a field of mathematics, the Hausdorff density measures how concentrated a Radon measure
is at some point.
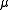be a Radon measure and 
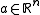some point in Euclidean space
. The s-dimensional upper and lower Hausdorff densities are defined to be, respectively,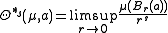
and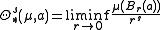
where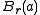
is the ball of radius r > 0 centered at a. Clearly, 
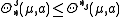for all 
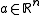. In the event that the two are equal, we call their common value the s-density of 
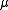at a and denote it 
.
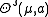s.
Radon measure
In mathematics , a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological space X that is locally finite and inner regular.-Motivation:...
is at some point.
Definition
Let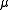 be a Radon measure and 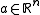some point in Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. The s-dimensional upper and lower Hausdorff densities are defined to be, respectively,
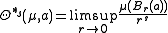
and
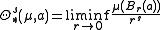
where
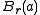is the ball of radius r > 0 centered at a. Clearly, 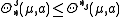for all 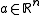. In the event that the two are equal, we call their common value the s-density of 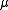at a and denote it 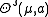.Marstrand's theorem
The following theorem states that the times when the s-density exists are rather seldom.- Marstrand's theorem: Let
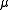be a Radon measure on 
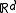. Suppose that the s-density 
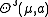exists and is positive and finite for a in a set of positive 
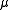measure. Then s is an integer.
Preiss' theorem
In 1987 Preiss proved a stronger version of Marstrand's theorem. One consequence is that that sets with positive and finite density are rectifiable setRectifiable set
In mathematics, a rectifiable set is a set that is smooth in a certain measure-theoretic sense. It is an extension of the idea of a rectifiable curve to higher dimensions; loosely speaking, a rectifiable set is a rigorous formulation of a piece-wise smooth set...
s.
- Preiss' theorem: Let
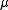be a Radon measure on 
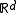. Suppose that m
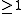is an integer and the m-density 
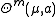exists and is positive and finite for 
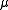almost every a in the supportSupport (measure theory)In mathematics, the support of a measure μ on a measurable topological space is a precise notion of where in the space X the measure "lives"...
of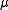
. Then 
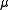is m-rectifiable, i.e. 
(
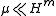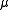is absolutely continuous with respect to Hausdorff measureHausdorff measureIn mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
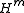) and the support of 
is an m-rectifiable set.