Hawaiian earring
Encyclopedia
In mathematics
, the Hawaiian earring H is the topological space
defined by the union
of circles in the Euclidean plane R2 with center (1/n, 0) and radius 1/n for n = 1, 2, 3, .... The space H is homeomorphic
to the one-point compactification of the union of a countably infinite family of open intervals
.
The Hawaiian earring can be given a complete metric
and it is compact
. It is path connected but not semilocally simply connected.
The Hawaiian earring looks very similar to the wedge sum
of countably infinitely many circles; that is, the rose with infinitely many petals, but those two spaces are not homeomorphic. The difference between their topologies is seen in the fact that, in the Hawaiian earring, every open neighborhood of the point of intersection of the circles contains all but finitely many of the circles. It is also seen in the fact that the wedge sum is not compact: the complement of the distinguished point is a union of open intervals; to those add a small open neighborhood of the distinguished point to get an open cover with no finite subcover.
G.
The Hawaiian earring H has the free group
of countably infinitely many generators as a proper subgroup of its fundamental group
. G contains additional elements which arise from loops whose image is not contained in finitely many of the Hawaiian's earrings circles; in fact, some of them are surjective. For example, the path that on the interval [2−n, 2−(n−1)] circumnavigates the nth circle.
It has been shown that G embeds
into the inverse limit
of the free groups with n generators, Fn, where the bonding map from Fn to Fn−1 simply kills the last generator of Fn. However G is not the complete inverse limit but rather the subgroup in which each generator appears only finitely many times. An example of an element of the inverse limit which is not an element of G is an infinite commutator.
G is uncountable, and it is not a free group. While its abelianisation has no known simple description, G has a normal subgroup N such that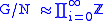
, the direct product
of infinitely many copies of the infinite cyclic group (the Baer–Specker group
). This is called the infinite abelianization or strong abelianization of the Hawaiian earring, since the subgroup N is generated by elements where each coordinate (thinking of the Hawaiian earring as a subgroup of the inverse limit) is a product of commutators. In a sense, N can be thought of as the closure of the commutator subgroup.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Hawaiian earring H is the topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
defined by the union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of circles in the Euclidean plane R2 with center (1/n, 0) and radius 1/n for n = 1, 2, 3, .... The space H is homeomorphic
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
to the one-point compactification of the union of a countably infinite family of open intervals
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
.
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
and it is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
. It is path connected but not semilocally simply connected.
The Hawaiian earring looks very similar to the wedge sum
Wedge sum
In topology, the wedge sum is a "one-point union" of a family of topological spaces. Specifically, if X and Y are pointed spaces the wedge sum of X and Y is the quotient of the disjoint union of X and Y by the identification x0 ∼ y0:X\vee Y = \;/ \sim,\,where ∼ is the...
of countably infinitely many circles; that is, the rose with infinitely many petals, but those two spaces are not homeomorphic. The difference between their topologies is seen in the fact that, in the Hawaiian earring, every open neighborhood of the point of intersection of the circles contains all but finitely many of the circles. It is also seen in the fact that the wedge sum is not compact: the complement of the distinguished point is a union of open intervals; to those add a small open neighborhood of the distinguished point to get an open cover with no finite subcover.
Fundamental group
The Hawaiian earring is not simply connected, since the loop parametrising any circle is not homotopic to a trivial loop. Thus, it has a nontrivial fundamental groupFundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
G.
The Hawaiian earring H has the free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
of countably infinitely many generators as a proper subgroup of its fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
. G contains additional elements which arise from loops whose image is not contained in finitely many of the Hawaiian's earrings circles; in fact, some of them are surjective. For example, the path that on the interval [2−n, 2−(n−1)] circumnavigates the nth circle.
It has been shown that G embeds
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
into the inverse limit
Inverse limit
In mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
of the free groups with n generators, Fn, where the bonding map from Fn to Fn−1 simply kills the last generator of Fn. However G is not the complete inverse limit but rather the subgroup in which each generator appears only finitely many times. An example of an element of the inverse limit which is not an element of G is an infinite commutator.
G is uncountable, and it is not a free group. While its abelianisation has no known simple description, G has a normal subgroup N such that
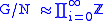, the direct productDirect product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
of infinitely many copies of the infinite cyclic group (the Baer–Specker group
Baer–Specker group
In mathematics, in the field of group theory, the Baer–Specker group, or Specker group, is an example of an infinite Abelian group which is a building block in the structure theory of such groups.-Definition:...
). This is called the infinite abelianization or strong abelianization of the Hawaiian earring, since the subgroup N is generated by elements where each coordinate (thinking of the Hawaiian earring as a subgroup of the inverse limit) is a product of commutators. In a sense, N can be thought of as the closure of the commutator subgroup.