Hawking energy
Encyclopedia
The Hawking energy or Hawking mass is one of the possible definitions of mass in general relativity
. It is a measure of the bending of ingoing and outgoing rays of light
that are orthogonal to a 2-sphere
surrounding the region of space whose mass is to be defined.
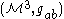be a 3-dimensional sub-manifold of a relativistic spacetime, and let 
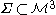be a closed 2-surface. Then the Hawking mass 
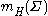of 
is defined to be
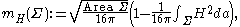
where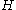
is the mean curvature
of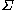
.
, the Hawking mass of any sphere
about the central mass is equal to the value 
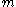of the central mass.
A result of Geroch implies that Hawking mass satisfies an important monotonicity condition. Namely, if
has nonnegative scalar curvature, then the Hawking mass of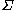 
is non-decreasing as the surface 
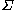flows outward at a speed equal to the inverse of the mean curvature. In particular, if 
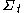is a family of connected surfaces evolving according to
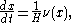
where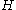
is the mean curvature of 
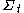and 
is the unit vector opposite of the mean curvature direction, then
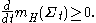
Hawking mass is also monotonically increasing for the inverse mean curvature flow
.
Hawking mass is not necessarily positive. However, it is asymptotic to the ADM or the Bondi mass, depending on whether the surface is asymptotic to spatial infinity or null infinity.
Mass in General Relativity
The concept of mass in general relativity is more complex than the concept of mass in special relativity. In fact, general relativity does not offer a single definition for the term mass, but offers several different definitions which are applicable under different circumstances...
. It is a measure of the bending of ingoing and outgoing rays of light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
that are orthogonal to a 2-sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
surrounding the region of space whose mass is to be defined.
Definition
Let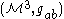 be a 3-dimensional sub-manifold of a relativistic spacetime, and let 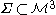be a closed 2-surface. Then the Hawking mass 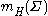of is defined to be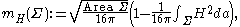where
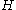is the mean curvatureMean curvature
In mathematics, the mean curvature H of a surface S is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space....
of
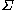.Properties
In the Schwarzschild metricSchwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
, the Hawking mass of any sphere
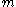about the central mass is equal to the value of the central mass.A result of Geroch implies that Hawking mass satisfies an important monotonicity condition. Namely, if
has nonnegative scalar curvature, then the Hawking mass of 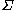is non-decreasing as the surface 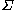flows outward at a speed equal to the inverse of the mean curvature. In particular, if 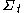is a family of connected surfaces evolving according to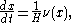where
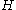is the mean curvature of 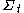and is the unit vector opposite of the mean curvature direction, then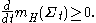Hawking mass is also monotonically increasing for the inverse mean curvature flow
Inverse mean curvature flow
In the field of differential geometry in mathematics, inverse mean curvature flow is an example of a geometric flow of hypersurfaces a Riemannian manifold...
.
Hawking mass is not necessarily positive. However, it is asymptotic to the ADM or the Bondi mass, depending on whether the surface is asymptotic to spatial infinity or null infinity.