Heisler Chart
Encyclopedia
Heisler Charts are a set of two charts per included geometry introduced in 1947 by M. P. Heisler which were supplemented by a third chart per geometry in 1961 by H. Gröber. They are used to provide a graphical analysis tool for the evaluation the central temperature for transient heat conduction
through an infinitely long plane wall of thickness 2L, an infinitely long cylinder of radius ro, and a sphere of radius ro.
Though the Heisler-Gröber Charts are a faster and simpler alternative to the exact solutions of these problems, there are some limitations. First, the body must be at uniform temperature initially. Additionally, the temperature of the surroundings and the convective heat transfer coefficient must remain constant and uniform. Also, there must be no heat generation from the body itself.
solution for an infinite plane wall:
,
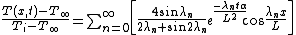where Ti is the initial temperature of the slab, T∞ is the constant temperature imposed at the boundary, x is the location in the plane wall, λn is π(n+1/2), and α is thermal diffusivity
. The position x=0 represents the center of the slab.
The first chart for the plane wall is plotted using 3 different variables. Plotted along the vertical axis of the chart is dimensionless temperature at the midplane, θo*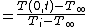
. Plotted along the horizontal axis is the Fourier Number, Fo=αt/L2 . The curves within the graph are a selection of values for the inverse of the Biot Number
, where "Bi = hL/k. k is the thermal conductivity of the material and h is the heat transfer coefficient."
The second chart is used to determine the variation of temperature within the plane wall for different Biot Numbers. The vertical axis is the ratio of a given temperature to that at the centerline θ/θo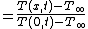
where the x/L curve is the position at which T is taken. The horizontal axis is the value of Bi−1.
The third chart in each set was supplemented by Gröber in 1961 and this particular one shows the dimensionless heat transferred from the wall as a function of a dimensionless time variable. The vertical axis is a plot of Q/Qo , the ratio of actual heat transfer to the amount of total possible heat transfer before T=T∞ . On the horizontal axis is the plot of (Bi2)(Fo), a dimensionless time variable.
.
Each chart plots similar curves to the previous examples, and on each axis is plotted a similar variable.
solution:
These charts can be used similar to the first two sets and are plots of similar variables.
Heat conduction
In heat transfer, conduction is a mode of transfer of energy within and between bodies of matter, due to a temperature gradient. Conduction means collisional and diffusive transfer of kinetic energy of particles of ponderable matter . Conduction takes place in all forms of ponderable matter, viz....
through an infinitely long plane wall of thickness 2L, an infinitely long cylinder of radius ro, and a sphere of radius ro.
Though the Heisler-Gröber Charts are a faster and simpler alternative to the exact solutions of these problems, there are some limitations. First, the body must be at uniform temperature initially. Additionally, the temperature of the surroundings and the convective heat transfer coefficient must remain constant and uniform. Also, there must be no heat generation from the body itself.
Infinitely Long Plane Wall (of thickness 2L)
These first Heisler-Gröber Charts were based upon the first term of the exact Fourier SeriesFourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
solution for an infinite plane wall:
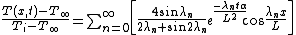,where Ti is the initial temperature of the slab, T∞ is the constant temperature imposed at the boundary, x is the location in the plane wall, λn is π(n+1/2), and α is thermal diffusivity
Thermal diffusivity
In heat transfer analysis, thermal diffusivity is the thermal conductivity divided by density and specific heat capacity at constant pressure. It has the SI unit of m²/s...
. The position x=0 represents the center of the slab.
The first chart for the plane wall is plotted using 3 different variables. Plotted along the vertical axis of the chart is dimensionless temperature at the midplane, θo*
. Plotted along the horizontal axis is the Fourier Number, Fo=αt/L2 . The curves within the graph are a selection of values for the inverse of the Biot NumberBiot number
The Biot number is a dimensionless number used in non-steady-state heat transfer calculations. It is named after the French physicist Jean-Baptiste Biot , and gives a simple index of the ratio of the heat transfer resistances inside of and at the surface of a body...
, where "Bi = hL/k. k is the thermal conductivity of the material and h is the heat transfer coefficient."
The second chart is used to determine the variation of temperature within the plane wall for different Biot Numbers. The vertical axis is the ratio of a given temperature to that at the centerline θ/θo
where the x/L curve is the position at which T is taken. The horizontal axis is the value of Bi−1.The third chart in each set was supplemented by Gröber in 1961 and this particular one shows the dimensionless heat transferred from the wall as a function of a dimensionless time variable. The vertical axis is a plot of Q/Qo , the ratio of actual heat transfer to the amount of total possible heat transfer before T=T∞ . On the horizontal axis is the plot of (Bi2)(Fo), a dimensionless time variable.
Infinitely Long Cylinder (of radius ro)
For the infinitely long cylinder, the Heisler chart is based on the first term in an exact solution to a Bessel functionBessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
.
Each chart plots similar curves to the previous examples, and on each axis is plotted a similar variable.
Sphere (of radius ro)
The Heisler Chart for a sphere is based on the first term in the exact Fourier seriesFourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
solution:
These charts can be used similar to the first two sets and are plots of similar variables.
Modern Alternatives
Currently there are programs that provide numerical solutions to the same problems, without using transcendental functions or infinite series. Examples of these programs can be found here or here.See also
- Convective heat transferConvective heat transferConvective heat transfer, often referred to as convection, is the transfer of heat from one place to another by the movement of fluids. The presence of bulk motion of the fluid enhances the heat transfer between the solid surface and the fluid. Convection is usually the dominant form of heat...
- Heat transfer coefficient
- Biot numberBiot numberThe Biot number is a dimensionless number used in non-steady-state heat transfer calculations. It is named after the French physicist Jean-Baptiste Biot , and gives a simple index of the ratio of the heat transfer resistances inside of and at the surface of a body...
- Fourier numberFourier numberIn physics and engineering, the Fourier number or Fourier modulus, named after Joseph Fourier, is a dimensionless number that characterizes heat conduction. Conceptually, it is the ratio of the heat conduction rate to the rate of thermal energy storage. Together with the Biot number, it...
- heat conductionHeat conductionIn heat transfer, conduction is a mode of transfer of energy within and between bodies of matter, due to a temperature gradient. Conduction means collisional and diffusive transfer of kinetic energy of particles of ponderable matter . Conduction takes place in all forms of ponderable matter, viz....