
Helicopter Cube
Encyclopedia
The Helicopter Cube is a Rubik's Cube
-like puzzle invented by Adam G. Cowan in 2005 and built in 2006. It is also in the shape of a cube
, but cut differently, and twists around cube edges rather than cube faces. The purpose of the puzzle is to scramble the colors, and then restore them back to their original state of a single color per face.
There are two variants of the Helicopter Cube: the one manufactured by The Twisty Store (sold also by Uwe Mèffert
), consisting only of 8 corner pieces and 24 face center pieces, and the "Curvy Copter" by Tom van der Zanden, which has an additional 12 edge pieces with 2 colors each.
When twisting the puzzle, a 180° turn exchanges two corner pieces and swaps two pairs of face center pieces, but preserves the cube shape. The entire puzzle can be scrambled in this way.
However, it is also possible to twist an edge by ~71°, such that the base of two groups of a corner piece and a face center piece each is aligned with the rotational plane of a different edge. The second edge can then be rotated, thus intermixing the corner pieces and the face center pieces and leaving the puzzle in a non-cubical shape. This kind of intermixing is known as a jumbling move. Due to the differing shapes of the intermixed pieces, some rotations possible in the cubical shape may no longer be possible in the jumbled shape. By using a combination of such "jumbling" moves, it is possible to return to cubical shape but with some face center pieces in the wrong orientation, thus jutting outwards like spikes rather than lie flat on the face of the cube. More subtle changes may also be introduced, which are described later.
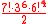 combinations.
combinations.
The expanded number is 493 694 233 804 800 000 (approximately four hundred ninety four quadrillion).
Rubik's Cube
Rubik's Cube is a 3-D mechanical puzzle invented in 1974 by Hungarian sculptor and professor of architecture Ernő Rubik.Originally called the "Magic Cube", the puzzle was licensed by Rubik to be sold by Ideal Toy Corp. in 1980 and won the German Game of the Year special award for Best Puzzle that...
-like puzzle invented by Adam G. Cowan in 2005 and built in 2006. It is also in the shape of a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
, but cut differently, and twists around cube edges rather than cube faces. The purpose of the puzzle is to scramble the colors, and then restore them back to their original state of a single color per face.
Description
The Helicopter Cube is made in the shape of a cube, cut into 8 corner pieces and 24 face center pieces. Each corner piece has 3 colors, and each face center piece has only a single color. Unlike the Rubik's Cube, its faces do not rotate; rather, the pieces are scrambled by rotating around a cube edge.There are two variants of the Helicopter Cube: the one manufactured by The Twisty Store (sold also by Uwe Mèffert
Uwe Mèffert
Uwe Mèffert has manufactured and sold mechanical puzzles in the style of Rubik's Cube since the original Cube craze. His first design was the Pyraminx and others include the Megaminx, Skewb and Skewb Diamond...
), consisting only of 8 corner pieces and 24 face center pieces, and the "Curvy Copter" by Tom van der Zanden, which has an additional 12 edge pieces with 2 colors each.
When twisting the puzzle, a 180° turn exchanges two corner pieces and swaps two pairs of face center pieces, but preserves the cube shape. The entire puzzle can be scrambled in this way.
However, it is also possible to twist an edge by ~71°, such that the base of two groups of a corner piece and a face center piece each is aligned with the rotational plane of a different edge. The second edge can then be rotated, thus intermixing the corner pieces and the face center pieces and leaving the puzzle in a non-cubical shape. This kind of intermixing is known as a jumbling move. Due to the differing shapes of the intermixed pieces, some rotations possible in the cubical shape may no longer be possible in the jumbled shape. By using a combination of such "jumbling" moves, it is possible to return to cubical shape but with some face center pieces in the wrong orientation, thus jutting outwards like spikes rather than lie flat on the face of the cube. More subtle changes may also be introduced, which are described later.
Solutions
If the puzzle is only scrambled using 180° twists, then it is obviously solvable using only 180° twists. However, if some jumbling moves were made, even if the puzzle was subsequently returned to cube shape, it may not be possible to solve it using only 180° twists. The reason for this is that using only 180° twists, each face center piece can only be permuted within a 6-member cycle, often referred to as its orbit. Face center pieces in different orbits cannot be interchanged using only 180° twists. However, jumbling moves are able to permute face center pieces between different orbits, thus leaving the puzzle in a state that cannot be solved by 180° twists alone.Number of combinations
The Helicopter Cube has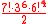 combinations.
combinations.The expanded number is 493 694 233 804 800 000 (approximately four hundred ninety four quadrillion).

