
Helly's theorem
Encyclopedia
Helly's theorem is a basic result in discrete geometry
describing the ways that convex set
s may intersect
each other. It was discovered by Eduard Helly
in 1913, but not published by him until 1923, by which time alternative proofs by and had already appeared. Helly's theorem gave rise to the notion of a Helly family
.
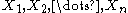
is a finite collection of convex subsets of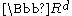 , where
, where 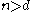 . If the intersection of every
. If the intersection of every 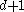 of these sets is nonempty, then the whole collection has a nonempty intersection; that is,
of these sets is nonempty, then the whole collection has a nonempty intersection; that is,
For infinite collections one has to assume compactness: If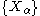 is a collection of compact convex subsets of
is a collection of compact convex subsets of 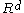 and every subcollection of cardinality at most
and every subcollection of cardinality at most 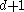 has nonempty intersection, then the whole collection has nonempty intersection.
has nonempty intersection, then the whole collection has nonempty intersection.
as in the proof by . The infinite version then follows by the finite intersection property
characterization of compactness
: a collection of closed subsets of a compact space has a non-empty intersection if and only if every finite subcollection has a non-empty intersection (once you fix a single set, the intersection of all others with it are closed subsets of a fixed compact space).
Suppose first that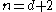 . By our assumptions, there is a point
. By our assumptions, there is a point
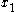 that is in the common intersection of
that is in the common intersection of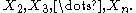
Likewise, for every
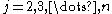
there is a point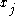 that is in the
that is in the
common intersection of all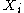 with the possible exception of
with the possible exception of 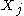 .
.
We now apply Radon's theorem
to the set
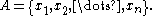
Radon's theorem tells us that there are disjoint subsets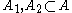 such that the
such that the
convex hull
of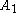 intersects the convex hull of
intersects the convex hull of 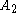 . Suppose that
. Suppose that 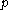 is a point in the intersection of these two convex hulls. We claim that
is a point in the intersection of these two convex hulls. We claim that
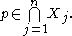
Indeed, consider any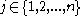 . Note that the only element of
. Note that the only element of 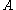 that is not
that is not
in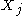 is
is 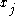 . If
. If 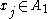 , then
, then 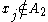 , and therefore
, and therefore 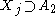 .
.
Since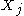 is convex, it then also contains the convex hull of
is convex, it then also contains the convex hull of 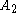 and therefore also
and therefore also 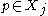 .
.
Likewise, if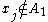 , then
, then 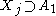 , and by the same reasoning
, and by the same reasoning 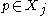 .
.
Since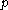 is in every
is in every 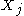 , it must also be in the intersection.
, it must also be in the intersection.
Above, we have assumed that the points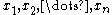 are all distinct. If this is not the case,
are all distinct. If this is not the case,
say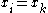 for some
for some 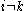 , then
, then 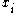 is in every one of the sets
is in every one of the sets 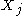 , and again we conclude that the intersection is nonempty. This completes the proof in the case
, and again we conclude that the intersection is nonempty. This completes the proof in the case 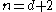 .
.
Now suppose that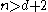 and that the statement is true for
and that the statement is true for  , by induction.
, by induction.
The above argument shows that any subcollection of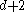 sets will have nonempty intersection.
sets will have nonempty intersection.
We may then consider the collection where we replace the two sets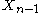 and
and 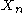
with the single set
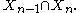
In this new collection, every subcollection of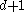 sets will
sets will
have nonempty intersection. The inductive hypothesis therefore applies, and shows that this
new collection has nonempty intersection. This implies the same for the original collection, and completes the proof.
Discrete geometry
Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles,...
describing the ways that convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
s may intersect
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
each other. It was discovered by Eduard Helly
Eduard Helly
Eduard Helly was a mathematician and the eponym of Helly's theorem, Helly families, Helly's selection theorem, Helly metric, and the Helly–Bray theorem. In 1912, Helly published a proof of Hahn–Banach theorem, 15 years before Hahn and Banach discovered it independently...
in 1913, but not published by him until 1923, by which time alternative proofs by and had already appeared. Helly's theorem gave rise to the notion of a Helly family
Helly family
In combinatorics, a Helly family of order k is a family of sets such that any minimal subfamily with an empty intersection has k or fewer sets in it. In other words, any subfamily such that every k-fold intersection is non-empty has non-empty total intersection.The k-Helly property is the property...
.
Statement
Suppose that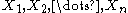
is a finite collection of convex subsets of
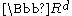 , where
, where 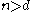 . If the intersection of every
. If the intersection of every 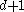 of these sets is nonempty, then the whole collection has a nonempty intersection; that is,
of these sets is nonempty, then the whole collection has a nonempty intersection; that is,
For infinite collections one has to assume compactness: If
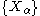 is a collection of compact convex subsets of
is a collection of compact convex subsets of 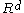 and every subcollection of cardinality at most
and every subcollection of cardinality at most 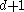 has nonempty intersection, then the whole collection has nonempty intersection.
has nonempty intersection, then the whole collection has nonempty intersection.Proof
We prove the finite version, using Radon's theoremRadon's theorem
In geometry, Radon's theorem on convex sets, named after Johann Radon, states that any set of d + 2 points in Rd can be partitioned into two sets whose convex hulls intersect...
as in the proof by . The infinite version then follows by the finite intersection property
Finite intersection property
In general topology, a branch of mathematics, the finite intersection property is a property of a collection of subsets of a set X. A collection has this property if the intersection over any finite subcollection of the collection is nonempty....
characterization of compactness
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
: a collection of closed subsets of a compact space has a non-empty intersection if and only if every finite subcollection has a non-empty intersection (once you fix a single set, the intersection of all others with it are closed subsets of a fixed compact space).
Suppose first that
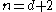 . By our assumptions, there is a point
. By our assumptions, there is a point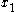 that is in the common intersection of
that is in the common intersection of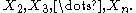
Likewise, for every
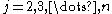
there is a point
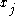 that is in the
that is in thecommon intersection of all
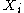 with the possible exception of
with the possible exception of 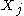 .
.We now apply Radon's theorem
Radon's theorem
In geometry, Radon's theorem on convex sets, named after Johann Radon, states that any set of d + 2 points in Rd can be partitioned into two sets whose convex hulls intersect...
to the set
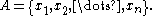
Radon's theorem tells us that there are disjoint subsets
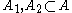 such that the
such that theconvex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of
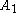 intersects the convex hull of
intersects the convex hull of 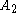 . Suppose that
. Suppose that 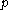 is a point in the intersection of these two convex hulls. We claim that
is a point in the intersection of these two convex hulls. We claim that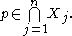
Indeed, consider any
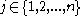 . Note that the only element of
. Note that the only element of 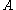 that is not
that is notin
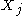 is
is 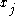 . If
. If 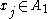 , then
, then 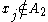 , and therefore
, and therefore 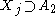 .
.Since
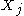 is convex, it then also contains the convex hull of
is convex, it then also contains the convex hull of 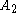 and therefore also
and therefore also 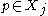 .
.Likewise, if
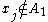 , then
, then 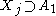 , and by the same reasoning
, and by the same reasoning 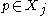 .
.Since
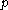 is in every
is in every 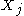 , it must also be in the intersection.
, it must also be in the intersection.Above, we have assumed that the points
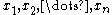 are all distinct. If this is not the case,
are all distinct. If this is not the case,say
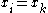 for some
for some 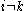 , then
, then 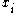 is in every one of the sets
is in every one of the sets 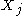 , and again we conclude that the intersection is nonempty. This completes the proof in the case
, and again we conclude that the intersection is nonempty. This completes the proof in the case 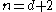 .
.Now suppose that
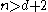 and that the statement is true for
and that the statement is true for  , by induction.
, by induction.The above argument shows that any subcollection of
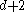 sets will have nonempty intersection.
sets will have nonempty intersection.We may then consider the collection where we replace the two sets
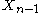 and
and 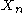
with the single set
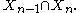
In this new collection, every subcollection of
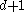 sets will
sets willhave nonempty intersection. The inductive hypothesis therefore applies, and shows that this
new collection has nonempty intersection. This implies the same for the original collection, and completes the proof.
See also
- Carathéodory's theoremCarathéodory's theorem (convex hull)In convex geometry Carathéodory's theorem states that if a point x of Rd lies in the convex hull of a set P, there is a subset P′ of P consisting of d+1 or fewer points such that x lies in the convex hull of P′. Equivalently, x lies in an r-simplex with vertices in P, where r \leq d...
- Shapley–Folkman lemmaShapley–Folkman lemmaIn geometry and economics, the Shapley–Folkman lemma describes the Minkowski addition of sets in a vector space. Minkowski addition is defined as the addition of the sets' members: for example, adding the set consisting of the integers zero and one to itself yields the set consisting of...
- Krein–Milman theorem
- Choquet theoryChoquet theoryIn mathematics, Choquet theory is an area of functional analysis and convex analysis created by Gustave Choquet. It is concerned with measures with support on the extreme points of a convex set C...
- Radon's theoremRadon's theoremIn geometry, Radon's theorem on convex sets, named after Johann Radon, states that any set of d + 2 points in Rd can be partitioned into two sets whose convex hulls intersect...

