Hermite constant
Encyclopedia
In mathematics
, the Hermite constant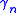
for integers n > 0, named after Charles Hermite
, is defined as follows. Given a lattice
L in Euclidean space
Rn,
let λ1(L) denote the least length of a nonzero element of L. Then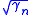
is the maximum of λ1(L) over all lattices L of unit covolume, i.e. vol(Rn/L) = 1.
The square root
in the definition of the Hermite constant is a matter of historical convention. With the definition as stated, it turns out that the Hermite constant grows linearly in n as n becomes unbounded.
Alternatively, the Hermite constant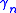
can be defined as the square of the maximal systole of a flat n-dimensional torus
of unit volume.
For n = 2, one has
. This value is attained by the Eisenstein integers.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Hermite constant
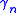for integers n > 0, named after Charles HermiteCharles Hermite
Charles Hermite was a French mathematician who did research on number theory, quadratic forms, invariant theory, orthogonal polynomials, elliptic functions, and algebra....
, is defined as follows. Given a lattice
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
L in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn,
let λ1(L) denote the least length of a nonzero element of L. Then
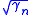is the maximum of λ1(L) over all lattices L of unit covolume, i.e. vol(Rn/L) = 1.The square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
in the definition of the Hermite constant is a matter of historical convention. With the definition as stated, it turns out that the Hermite constant grows linearly in n as n becomes unbounded.
Alternatively, the Hermite constant
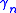can be defined as the square of the maximal systole of a flat n-dimensional torusTorus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
of unit volume.
Example
The Hermite constant is known in dimensions 1–8 and 24.For n = 2, one has
. This value is attained by the Eisenstein integers.