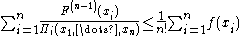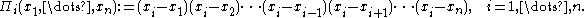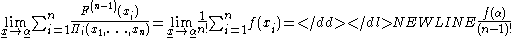Hermite–Hadamard inequality
Encyclopedia
In mathematics
, the Hermite–Hadamard inequality, named after Charles Hermite
and Jacques Hadamard
and sometimes also called Hadamard's inequality, states that if a function ƒ : [a, b] → R is convex
, then
One of the most natural extension of the right side of this classical enequality is due to Zoltán Retkes. For to formulate this result one has to introduce the notion of iterated integrals.
Under the above conditions the following sequence of functions is called the sequence of iterated integrals of f,where a ≤ s ≤ b.:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Hermite–Hadamard inequality, named after Charles Hermite
Charles Hermite
Charles Hermite was a French mathematician who did research on number theory, quadratic forms, invariant theory, orthogonal polynomials, elliptic functions, and algebra....
and Jacques Hadamard
Jacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
and sometimes also called Hadamard's inequality, states that if a function ƒ : [a, b] → R is convex
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
, then
One of the most natural extension of the right side of this classical enequality is due to Zoltán Retkes. For to formulate this result one has to introduce the notion of iterated integrals.
The concept of the sequence of iterated integrals
Suppose that −∞ < a < b < ∞, and let f:[a, b] → ℝ be an integrable real function.Under the above conditions the following sequence of functions is called the sequence of iterated integrals of f,where a ≤ s ≤ b.:
-
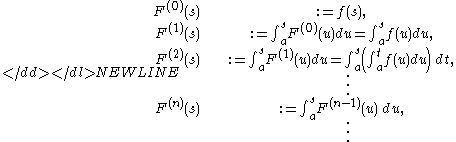
Example 1
Let [a, b] = [0, 1] and f(s) ≡ 1. Then the sequence of iterated integrals of 1 is defined on [0, 1], and
-
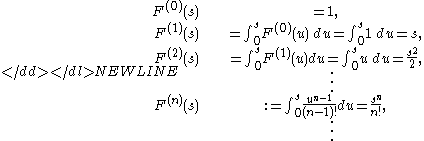
Example 2
Let [a,b] = [−1,1] and f(s) ≡ 1. Then the sequence of iterated integrals of 1 is defined on [−1, 1], and
-
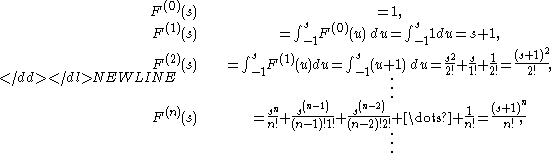
Example 3
Let [a, b] = [0, 1] and f(s) = es. Then the sequence of iterated integrals of f is defined on [0, 1], and
-
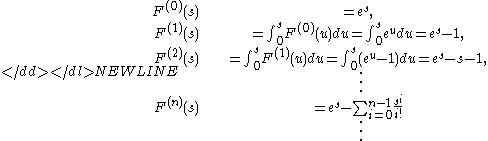
Theorem (Retkes inequality)
Suppose that −∞ < a < b < ∞, and let f:[a,b]→R be a convex function, a < xi < b, i = 1, ..., n, such that xi ≠ xj, if i ≠ j. Then the following holds:
where
In the concave case ≤ is changed to ≥.
Remark 1. If f is convex in the strict sense then ≤ is changed to < and equality holds iff f is linear function.
Remark 2. The inequality is sharp in the following limit sense: let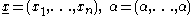 and
and 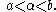
Then the limit of the left side exists and
-
-
-
-