
Hermitian wavelet
Encyclopedia
Hermitian wavelets are a family of continuous wavelets, used in the continuous wavelet transform
. The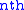 Hermitian wavelet is defined as the
Hermitian wavelet is defined as the 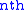 derivative of a Gaussian:
derivative of a Gaussian:
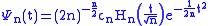
where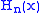 denotes the
denotes the 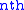 Hermite polynomial.
Hermite polynomial.
The normalisation coefficient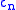 is given by:
is given by:
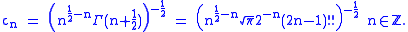
The prefactor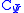 in the resolution of the identity of the continuous wavelet transform for this wavelet is given by:
in the resolution of the identity of the continuous wavelet transform for this wavelet is given by:
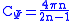
i.e. Hermitian wavelets are admissible for all positive .
.
In computer vision
and image processing
, Gaussian derivative operators of different orders are frequently used as a basis for expressing various types of visual operations; see scale-space and N-jet
.
Examples of Hermitian wavelets:
Starting from a Gaussian function with :
:
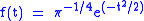
the first 3 derivatives read
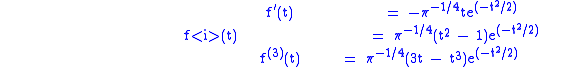
and their norms
norms 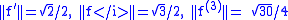
So the wavelets which are the negative normalized derivatives are:

Continuous wavelet transform
A continuous wavelet transform is used to divide a continuous-time function into wavelets. Unlike Fourier transform, the continuous wavelet transform possesses the ability to construct a time-frequency representation of a signal that offers very good time and frequency localization...
. The
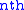 Hermitian wavelet is defined as the
Hermitian wavelet is defined as the 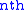 derivative of a Gaussian:
derivative of a Gaussian: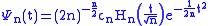
where
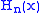 denotes the
denotes the 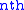 Hermite polynomial.
Hermite polynomial.The normalisation coefficient
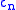 is given by:
is given by: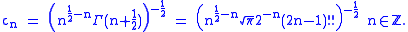
The prefactor
 in the resolution of the identity of the continuous wavelet transform for this wavelet is given by:
in the resolution of the identity of the continuous wavelet transform for this wavelet is given by: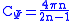
i.e. Hermitian wavelets are admissible for all positive
 .
.In computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
and image processing
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
, Gaussian derivative operators of different orders are frequently used as a basis for expressing various types of visual operations; see scale-space and N-jet
N-jet
An N-jet is the set of derivatives of a function f up to order N.Specifically, in the area of computer vision, the N-jet is usually computed from a scale-space representation L of the input image f, and the partial derivatives of L are used as a basis for expressing various types of visual modules...
.
Examples of Hermitian wavelets:
Starting from a Gaussian function with
 :
: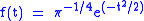
the first 3 derivatives read
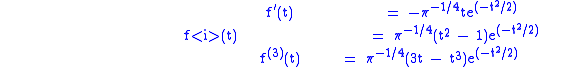
and their
 norms
norms 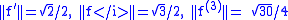
So the wavelets which are the negative normalized derivatives are:


