Herschel-Bulkley fluid
Encyclopedia
The Herschel–Bulkley fluid is a generalized model of a non-Newtonian fluid
, in which the strain
experienced by the fluid is related to the stress
in a complicated, non-linear way. Three parameters characterize this relationship: the consistency k, the flow index n, and the yield shear stress . The consistency is a simple constant of proportionality, while the flow index measures the degree to which the fluid is shear-thinning or shear-thickening. Ordinary paint is one example of a shear-thinning fluid, while oobleck provides one realization of a shear-thickening fluid. Finally, the yield stress quantifies the amount of stress that the fluid may experience before it yields and begins to flow.
. The consistency is a simple constant of proportionality, while the flow index measures the degree to which the fluid is shear-thinning or shear-thickening. Ordinary paint is one example of a shear-thinning fluid, while oobleck provides one realization of a shear-thickening fluid. Finally, the yield stress quantifies the amount of stress that the fluid may experience before it yields and begins to flow.
This non-Newtonian fluid model was introduced by Herschel and Bulkley in 1926.
is given, in the usual way, as a viscosity, multiplied by the rate-of-strain tensor:

where in contrast to the Newtonian fluid, the viscosity is itself a function of the strain tensor. This is constituted through the formula
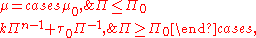
where is the second invariant of the rate-of-strain tensor:
is the second invariant of the rate-of-strain tensor:
 .
.
If n=1 and , this model reduces to the Newtonian fluid. If
, this model reduces to the Newtonian fluid. If  the fluid is shear-thinning, while
the fluid is shear-thinning, while  produces a shear-thickening fluid. The limiting viscosity
produces a shear-thickening fluid. The limiting viscosity 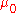 is chosen such that
is chosen such that  . A large limiting viscosity means that the fluid will only flow in response to a large applied force. This feature captures the Bingham-type behaviour of the fluid.
. A large limiting viscosity means that the fluid will only flow in response to a large applied force. This feature captures the Bingham-type behaviour of the fluid.
This equation is also commonly written as

where is the shear stress,
is the shear stress, 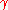 the shear rate,
the shear rate,  the yield stress, and K and n are regarded as model factors.
the yield stress, and K and n are regarded as model factors.
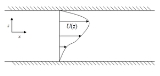
 A frequently-encountered situation in experiments is pressure
A frequently-encountered situation in experiments is pressure
-driven channel flow (see diagram). This situation exhibits an equilibrium in which there is flow only in the horizontal direction (along the pressure-gradient direction), and the pressure gradient and viscous effects are in balance. Then, the Navier-Stokes equations
, together with the rheological
model, reduce to a single equation:
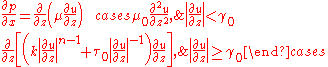
To solve this equation it is necessary to non-dimensionalize the quantities involved. The channel depth H is chosen as a length scale, the mean velocity V is taken as a velocity scale, and the pressure scale is taken to be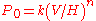 . This analysis introduces the non-dimensional pressure gradient
. This analysis introduces the non-dimensional pressure gradient
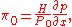
which is negative for flow from left to right, and the Bingham number:

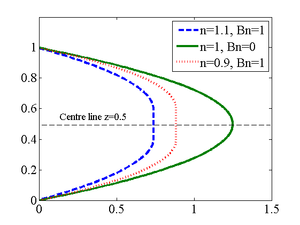
Next, the domain of the solution is broken up into three parts, valid for a negative pressure gradient:
Solving this equation gives the velocity profile:
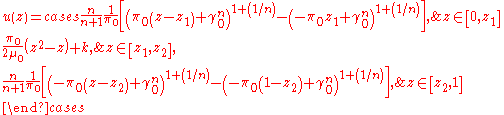
Here k is a matching constant such that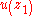 is continuous. The profile respects the no-slip
is continuous. The profile respects the no-slip
conditions at the channel boundaries,
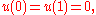
Using the same continuity arguments, it is shown that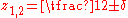 , where
, where

Since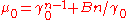 , for a given
, for a given 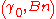 pair, there is a critical pressure gradient
pair, there is a critical pressure gradient
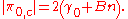
Apply any pressure gradient smaller in magnitude than this critical value, and the fluid will not flow; its Bingham nature is thus apparent. Any pressure gradient greater in magnitude than this critical value will result in flow. The flow associated with a shear-thickening fluid is retarded relative to that associated with a shear-thinning fluid.
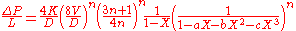
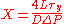
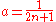
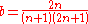
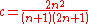
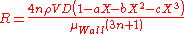
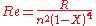
allows standard Newtonian friction factor correlations to be used.
Non-Newtonian fluid
A non-Newtonian fluid is a fluid whose flow properties differ in any way from those of Newtonian fluids. Most commonly the viscosity of non-Newtonian fluids is not independent of shear rate or shear rate history...
, in which the strain
Strain
Strain can refer to:* Strain , variants of plants, viruses or bacteria; or an inbred animal used for experimental purposes* Strain , a chemical stress of a molecule...
experienced by the fluid is related to the stress
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
in a complicated, non-linear way. Three parameters characterize this relationship: the consistency k, the flow index n, and the yield shear stress
 . The consistency is a simple constant of proportionality, while the flow index measures the degree to which the fluid is shear-thinning or shear-thickening. Ordinary paint is one example of a shear-thinning fluid, while oobleck provides one realization of a shear-thickening fluid. Finally, the yield stress quantifies the amount of stress that the fluid may experience before it yields and begins to flow.
. The consistency is a simple constant of proportionality, while the flow index measures the degree to which the fluid is shear-thinning or shear-thickening. Ordinary paint is one example of a shear-thinning fluid, while oobleck provides one realization of a shear-thickening fluid. Finally, the yield stress quantifies the amount of stress that the fluid may experience before it yields and begins to flow.This non-Newtonian fluid model was introduced by Herschel and Bulkley in 1926.
Definition
The viscous stress tensorStress tensor
Stress tensor may refer to:* Stress , in classical physics* Stress-energy tensor, in relativistic theories* Maxwell stress tensor, in electromagnetism...
is given, in the usual way, as a viscosity, multiplied by the rate-of-strain tensor:

where in contrast to the Newtonian fluid, the viscosity is itself a function of the strain tensor. This is constituted through the formula
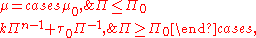
where
 is the second invariant of the rate-of-strain tensor:
is the second invariant of the rate-of-strain tensor: .
.If n=1 and
 , this model reduces to the Newtonian fluid. If
, this model reduces to the Newtonian fluid. If  the fluid is shear-thinning, while
the fluid is shear-thinning, while  produces a shear-thickening fluid. The limiting viscosity
produces a shear-thickening fluid. The limiting viscosity  is chosen such that
is chosen such that  . A large limiting viscosity means that the fluid will only flow in response to a large applied force. This feature captures the Bingham-type behaviour of the fluid.
. A large limiting viscosity means that the fluid will only flow in response to a large applied force. This feature captures the Bingham-type behaviour of the fluid.This equation is also commonly written as

where
 is the shear stress,
is the shear stress, 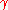 the shear rate,
the shear rate,  the yield stress, and K and n are regarded as model factors.
the yield stress, and K and n are regarded as model factors.Channel flow

Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
-driven channel flow (see diagram). This situation exhibits an equilibrium in which there is flow only in the horizontal direction (along the pressure-gradient direction), and the pressure gradient and viscous effects are in balance. Then, the Navier-Stokes equations
Navier-Stokes equations
In physics, the Navier–Stokes equations, named after Claude-Louis Navier and George Gabriel Stokes, describe the motion of fluid substances. These equations arise from applying Newton's second law to fluid motion, together with the assumption that the fluid stress is the sum of a diffusing viscous...
, together with the rheological
Rheology
Rheology is the study of the flow of matter, primarily in the liquid state, but also as 'soft solids' or solids under conditions in which they respond with plastic flow rather than deforming elastically in response to an applied force....
model, reduce to a single equation:

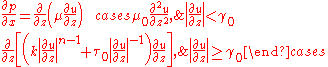
To solve this equation it is necessary to non-dimensionalize the quantities involved. The channel depth H is chosen as a length scale, the mean velocity V is taken as a velocity scale, and the pressure scale is taken to be
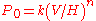 . This analysis introduces the non-dimensional pressure gradient
. This analysis introduces the non-dimensional pressure gradient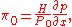
which is negative for flow from left to right, and the Bingham number:

Next, the domain of the solution is broken up into three parts, valid for a negative pressure gradient:
- A region close to the bottom wall where
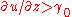 ;
; - A region in the fluid core where
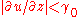 ;
; - A region close to the top wall where
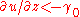 ,
,
Solving this equation gives the velocity profile:
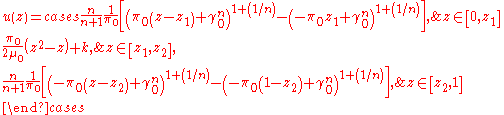
Here k is a matching constant such that
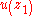 is continuous. The profile respects the no-slip
is continuous. The profile respects the no-slipNo-slip condition
In fluid dynamics, the no-slip condition for viscous fluids states that at a solid boundary, the fluid will have zero velocity relative to the boundary.The fluid velocity at all fluid–solid boundaries is equal to that of the solid boundary...
conditions at the channel boundaries,
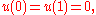
Using the same continuity arguments, it is shown that
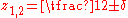 , where
, where
Since
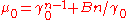 , for a given
, for a given 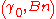 pair, there is a critical pressure gradient
pair, there is a critical pressure gradient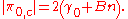
Apply any pressure gradient smaller in magnitude than this critical value, and the fluid will not flow; its Bingham nature is thus apparent. Any pressure gradient greater in magnitude than this critical value will result in flow. The flow associated with a shear-thickening fluid is retarded relative to that associated with a shear-thinning fluid.
Pipe flow
For laminar flow Chilton and Stainsby provide the following equation to calculate the pressure drop. The equation requires an iterative solution to extract the pressure drop, as it is present on both sides of the equation.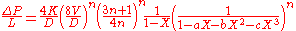
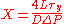
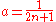
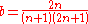
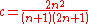
- For turbulent flow the authors propose a method that requires knowledge of the wall shear stress, but do not provide a method to calculate the wall shear stress. Their procedure is expanded in Hathoot
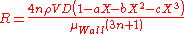
- All units are SI
 Pressure drop, Pa.
Pressure drop, Pa.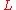 Pipe length, m
Pipe length, m Pipe diameter, m
Pipe diameter, m Fluid velocity,
Fluid velocity, 
- Chilton and Stainsby state that defining the Reynolds number as
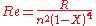
allows standard Newtonian friction factor correlations to be used.



