
Herzog-Schönheim conjecture
Encyclopedia
In mathematics
, the Herzog–Schönheim conjecture is a combinatorial problem in the area of group theory
.
Let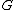 be a group
be a group
, and let
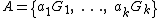
be a finite system of left cosets
of subgroup
s
 of
of 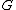 .
.
In 1974 M. Herzog and J. Schönheim conjectured
that if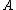 forms a partition
forms a partition
of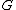
with ,
,
then the (finite) indices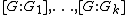 cannot be distinct. In contrast, if
cannot be distinct. In contrast, if 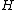 is a subgroup of
is a subgroup of 
with index
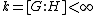 then
then 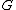 can be partitioned into
can be partitioned into 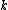 left cosets of
left cosets of  .
.
When is the additive group
is the additive group 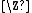 of integers, this is a conjecture of Paul Erdős
of integers, this is a conjecture of Paul Erdős
confirmed by H. Davenport
, L. Mirsky, D. Newman and R. Rado
independently. Observe that
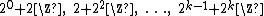
are pairwise disjoint with the indices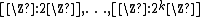 distinct, but they do not cover multiples of
distinct, but they do not cover multiples of 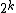 .
.
In 2004 Zhi-Wei Sun
proved an extended version
of the Herzog–Schönheim conjecture in the case where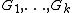 are subnormal
are subnormal
in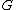
http://arxiv.org/abs/math/0306099. A basic lemma in Sun's proof states that if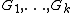 are subnormal and of finite index in
are subnormal and of finite index in 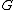 , then
, then
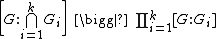
and hence
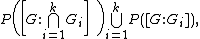
where denotes the set of prime
denotes the set of prime
divisor
s of .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Herzog–Schönheim conjecture is a combinatorial problem in the area of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
.
Let
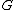 be a group
be a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, and let
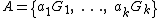
be a finite system of left cosets
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
of subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s
 of
of  .
.In 1974 M. Herzog and J. Schönheim conjectured
that if
 forms a partition
forms a partitionPartition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of
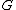
with
 ,
,then the (finite) indices
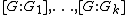 cannot be distinct. In contrast, if
cannot be distinct. In contrast, if 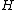 is a subgroup of
is a subgroup of 
with index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
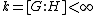 then
then 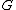 can be partitioned into
can be partitioned into 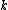 left cosets of
left cosets of  .
.When
 is the additive group
is the additive group 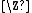 of integers, this is a conjecture of Paul Erdős
of integers, this is a conjecture of Paul ErdősPaul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
confirmed by H. Davenport
Harold Davenport
Harold Davenport FRS was an English mathematician, known for his extensive work in number theory.-Early life:...
, L. Mirsky, D. Newman and R. Rado
Richard Rado
Richard Rado FRS was a Jewish German mathematician. He earned two Ph.D.s: in 1933 from the University of Berlin, and in 1935 from the University of Cambridge. He was interviewed in Berlin by Lord Cherwell for a scholarship given by the chemist Sir Robert Mond which provided financial support to...
independently. Observe that
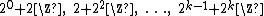
are pairwise disjoint with the indices
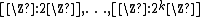 distinct, but they do not cover multiples of
distinct, but they do not cover multiples of 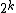 .
.In 2004 Zhi-Wei Sun
Zhi-Wei Sun
Zhi-Wei Sun is a Chinese mathematician, working primarily on number theory, combinatorics, and group theory. Currently he works as a professor in Nanjing University....
proved an extended version
of the Herzog–Schönheim conjecture in the case where
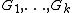 are subnormal
are subnormalSubnormal subgroup
In mathematics, in the field of group theory, a subgroup H of a given group G is a subnormal subgroup of G if there is a finite chain of subgroups of the group, each one normal in the next, beginning at H and ending at G....
in
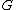
http://arxiv.org/abs/math/0306099. A basic lemma in Sun's proof states that if
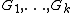 are subnormal and of finite index in
are subnormal and of finite index in 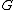 , then
, then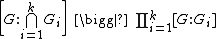
and hence
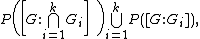
where
 denotes the set of prime
denotes the set of primePrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
s of
 .
.

