
Subnormal subgroup
Encyclopedia
In mathematics
, in the field of group theory
, a subgroup
H of a given group
G is a subnormal subgroup of G if there is a finite chain of subgroups of the group, each one normal
in the next, beginning at H and ending at G.
In notation, is
is 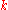 -subnormal in
-subnormal in  if there are subgroups
if there are subgroups

of such that
such that  is normal in
is normal in  for each
for each 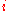 .
.
A subnormal subgroup is a subgroup that is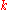 -subnormal for some positive integer
-subnormal for some positive integer 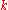 .
.
Some facts about subnormal subgroups:
The property of subnormality is transitive
, that is, a subnormal subgroup of a subnormal
subgroup is subnormal. In fact, the relation of subnormality can be defined as the transitive closure
of the relation of normality.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the field of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
H of a given group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G is a subnormal subgroup of G if there is a finite chain of subgroups of the group, each one normal
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
in the next, beginning at H and ending at G.
In notation,
 is
is 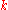 -subnormal in
-subnormal in  if there are subgroups
if there are subgroups
of
 such that
such that  is normal in
is normal in  for each
for each 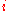 .
.A subnormal subgroup is a subgroup that is
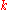 -subnormal for some positive integer
-subnormal for some positive integer 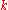 .
.Some facts about subnormal subgroups:
- A 1-subnormal subgroup is a proper normal subgroupNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
(and vice versa). - A finitely generated group is nilpotentNilpotent groupIn mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
if and only if each of its subgroups is subnormal. - Every quasinormal subgroupQuasinormal subgroupIn mathematics, in the field of group theory, a quasinormal subgroup, or permutable subgroup, is a subgroup of a group that commutes with every other subgroup...
, and, more generally, every conjugate permutable subgroupConjugate permutable subgroupIn mathematics, in the field of group theory, a conjugate-permutable subgroup is a subgroup that commutes with all its conjugate subgroups. The term was introduced by Tuval Foguel in 1996 and arose in the context of the proof that for finite groups, every quasinormal subgroup is a subnormal...
, of a finite group is subnormal. - Every pronormal subgroupPronormal subgroupIn mathematics, especially in the field of group theory, a pronormal subgroup is a subgroup that is embedded in a nice way. Pronormality is a simultaneous generalization of both normal subgroups and abnormal subgroups such as Sylow subgroups, ....
that is also subnormal, is, in fact, normal. In particular, a Sylow subgroup is subnormal if and only if it is normal. - Every 2-subnormal subgroup is a conjugate permutable subgroupConjugate permutable subgroupIn mathematics, in the field of group theory, a conjugate-permutable subgroup is a subgroup that commutes with all its conjugate subgroups. The term was introduced by Tuval Foguel in 1996 and arose in the context of the proof that for finite groups, every quasinormal subgroup is a subnormal...
.
The property of subnormality is transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
, that is, a subnormal subgroup of a subnormal
subgroup is subnormal. In fact, the relation of subnormality can be defined as the transitive closure
Transitive closure
In mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
of the relation of normality.
See also
- Normal subgroupNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
- Characteristic subgroupCharacteristic subgroupIn mathematics, particularly in the area of abstract algebra known as group theory, a characteristic subgroup is a subgroup that is invariant under all automorphisms of the parent group. Because conjugation is an automorphism, every characteristic subgroup is normal, though not every normal...
- Normal core
- Normal closureNormal closureThe term normal closure is used in two senses in mathematics:* In group theory, the normal closure of a subset of a group is the smallest normal subgroup that contains the subset; see conjugate closure....
- Ascendant subgroupAscendant subgroupIn mathematics, in the field of group theory, a subgroup of a group is said to be ascendant if there is an ascending series starting from the subgroup and ending at the group, such that every term in the series is a normal subgroup of its successor....
- Descendant subgroupDescendant subgroupIn mathematics, in the field of group theory, a subgroup of a group is said to be descendant if there is a descending series starting from the subgroup and ending at the group, such that every term in the series is a normal subgroup of its predecessor....
- Serial subgroup

