
Quasinormal subgroup
Encyclopedia
In mathematics
, in the field of group theory
, a quasinormal subgroup, or permutable subgroup, is a subgroup
of a group
that commutes (permutes) with every other subgroup. The term quasinormal subgroup was introduced by Øystein Ore
in 1937.
Two subgroups are said to permute (or commute) if any element from the first
subgroup, times an element of the second subgroup, can be written as an element of the second
subgroup, times an element of the first subgroup. That is, and
and 
as subgroups of are said to commute if HK = KH, that is, any element of the form
are said to commute if HK = KH, that is, any element of the form 
with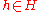 and
and  can be written in the form
can be written in the form 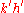
where and
and  .
.
Every quasinormal subgroup is a modular subgroup
, that is, a modular element in the lattice of subgroups
. This follows from the modular property of groups.
A conjugate permutable subgroup
is one that commutes with all its conjugate subgroups. Every quasinormal subgroup is conjugate permutable.
Every normal subgroup
is quasinormal, because, in fact, a normal subgroup commutes
with every element of the group. The converse is not true. For instance, any extension of a cyclic group of prime power order by another cyclic group of prime power order for the same prime, has the property that all its subgroups are quasinormal. However, not all of its subgroups need be normal.
Also, every quasinormal
subgroup of a finite group
is a subnormal subgroup
. This follows from the somewhat
stronger statement that every conjugate permutable subgroup is subnormal, which in turn
follows from the statement that every maximal conjugate permutable subgroup is normal. (The finiteness
is used crucially in the proofs.)
In any group, every quasinormal subgroup is ascendant
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the field of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a quasinormal subgroup, or permutable subgroup, is a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
that commutes (permutes) with every other subgroup. The term quasinormal subgroup was introduced by Øystein Ore
Øystein Ore
Øystein Ore was a Norwegian mathematician.-Life:Ore was graduated from the University of Oslo in 1922, with a Cand.Scient. degree in mathematics. In 1924, the University of Oslo awarded him the Ph.D. for a thesis titled Zur Theorie der algebraischen Körper, supervised by Thoralf Skolem...
in 1937.
Two subgroups are said to permute (or commute) if any element from the first
subgroup, times an element of the second subgroup, can be written as an element of the second
subgroup, times an element of the first subgroup. That is,
 and
and 
as subgroups of
 are said to commute if HK = KH, that is, any element of the form
are said to commute if HK = KH, that is, any element of the form 
with
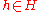 and
and  can be written in the form
can be written in the form 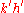
where
 and
and  .
.Every quasinormal subgroup is a modular subgroup
Modular subgroup
In mathematics, in the field of group theory, a modular subgroup is a subgroup that is a modular element in the lattice of subgroups, where the meet operation is defined by the intersection and the join operation is defined by the subgroup generated by the union of subgroups.By the Modular...
, that is, a modular element in the lattice of subgroups
Lattice of subgroups
In mathematics, the lattice of subgroups of a group G is the lattice whose elements are the subgroups of G, with the partial order relation being set inclusion....
. This follows from the modular property of groups.
A conjugate permutable subgroup
Conjugate permutable subgroup
In mathematics, in the field of group theory, a conjugate-permutable subgroup is a subgroup that commutes with all its conjugate subgroups. The term was introduced by Tuval Foguel in 1996 and arose in the context of the proof that for finite groups, every quasinormal subgroup is a subnormal...
is one that commutes with all its conjugate subgroups. Every quasinormal subgroup is conjugate permutable.
Every normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
is quasinormal, because, in fact, a normal subgroup commutes
with every element of the group. The converse is not true. For instance, any extension of a cyclic group of prime power order by another cyclic group of prime power order for the same prime, has the property that all its subgroups are quasinormal. However, not all of its subgroups need be normal.
Also, every quasinormal
subgroup of a finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
is a subnormal subgroup
Subnormal subgroup
In mathematics, in the field of group theory, a subgroup H of a given group G is a subnormal subgroup of G if there is a finite chain of subgroups of the group, each one normal in the next, beginning at H and ending at G....
. This follows from the somewhat
stronger statement that every conjugate permutable subgroup is subnormal, which in turn
follows from the statement that every maximal conjugate permutable subgroup is normal. (The finiteness
is used crucially in the proofs.)
In any group, every quasinormal subgroup is ascendant
Ascendant subgroup
In mathematics, in the field of group theory, a subgroup of a group is said to be ascendant if there is an ascending series starting from the subgroup and ending at the group, such that every term in the series is a normal subgroup of its successor....
.

