Hidden Markov random field
Encyclopedia
A hidden Markov random field is a generalization of a hidden Markov model
. Instead of having an underlying Markov chain
, hidden Markov random fields have an underlying Markov random field.
Suppose that we observe a random variable
, where 
.
Hidden Markov random fields assume that the probabilistic nature of
is determined
by the unobservable Markov random field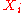
, 
.
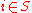That is, given the neighbors
of 
,
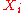is independent of all other 
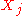(Markov property).
The main difference with a hidden Markov model
is that neighborhood is not defined in 1 dimension
but within a network, i.e.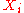
is allowed to have more than the two neighbors
that it would have in a Markov chain
.
The model is formulated in such a way that given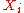
, 
are independent
(conditional independence of the observable variables given the Markov random field).
Hidden Markov model
A hidden Markov model is a statistical Markov model in which the system being modeled is assumed to be a Markov process with unobserved states. An HMM can be considered as the simplest dynamic Bayesian network. The mathematics behind the HMM was developed by L. E...
. Instead of having an underlying Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
, hidden Markov random fields have an underlying Markov random field.
Suppose that we observe a random variable
, where .Hidden Markov random fields assume that the probabilistic nature of
is determinedby the unobservable Markov random field
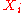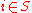, .That is, given the neighbors
of , 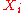is independent of all other 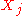(Markov property).The main difference with a hidden Markov model
Hidden Markov model
A hidden Markov model is a statistical Markov model in which the system being modeled is assumed to be a Markov process with unobserved states. An HMM can be considered as the simplest dynamic Bayesian network. The mathematics behind the HMM was developed by L. E...
is that neighborhood is not defined in 1 dimension
but within a network, i.e.
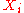is allowed to have more than the two neighborsthat it would have in a Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
.
The model is formulated in such a way that given
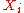, are independent(conditional independence of the observable variables given the Markov random field).