
Higman's lemma
Encyclopedia
In mathematics
, Higman's lemma states that the set of finite sequences over a finite alphabet, as partially ordered by the subsequence
relation, is well-quasi-ordered
. That is, if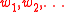 is an infinite sequence of words over some fixed finite alphabet, then there exist indices
is an infinite sequence of words over some fixed finite alphabet, then there exist indices  such that
such that 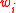 can be obtained from
can be obtained from 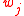 by deleting some (possibly none) symbols. More generally this remains true when the alphabet is not necessarily finite, but is itself well-quasi-ordered, and the subsequence relation allows the replacement of symbols by earlier symbols in the well-quasi-ordering of labels. This is a special case of the later Kruskal's tree theorem
by deleting some (possibly none) symbols. More generally this remains true when the alphabet is not necessarily finite, but is itself well-quasi-ordered, and the subsequence relation allows the replacement of symbols by earlier symbols in the well-quasi-ordering of labels. This is a special case of the later Kruskal's tree theorem
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Higman's lemma states that the set of finite sequences over a finite alphabet, as partially ordered by the subsequence
Subsequence
In mathematics, a subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements...
relation, is well-quasi-ordered
Well-quasi-ordering
In mathematics, specifically order theory, a well-quasi-ordering or wqo is a well-founded quasi-ordering with an additional restriction on sequences - that there is no infinite sequence x_i with x_i \not \le x_j for all i...
. That is, if
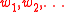 is an infinite sequence of words over some fixed finite alphabet, then there exist indices
is an infinite sequence of words over some fixed finite alphabet, then there exist indices  such that
such that 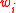 can be obtained from
can be obtained from 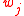 by deleting some (possibly none) symbols. More generally this remains true when the alphabet is not necessarily finite, but is itself well-quasi-ordered, and the subsequence relation allows the replacement of symbols by earlier symbols in the well-quasi-ordering of labels. This is a special case of the later Kruskal's tree theorem
by deleting some (possibly none) symbols. More generally this remains true when the alphabet is not necessarily finite, but is itself well-quasi-ordered, and the subsequence relation allows the replacement of symbols by earlier symbols in the well-quasi-ordering of labels. This is a special case of the later Kruskal's tree theoremKruskal's tree theorem
In mathematics, Kruskal's tree theorem states that the set of finite trees over a well-quasi-ordered set of labels is itself well-quasi-ordered...
.

