
Subsequence
Encyclopedia
In mathematics
, a subsequence is a sequence
that can be derived from another sequence by deleting some elements without changing the order of the remaining elements. For example, the sequence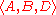 is a subsequence of
is a subsequence of 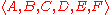 .
.
Given two sequences X and Y, a sequence G is said to be a common subsequence of X and Y, if G is a subsequence of both X and Y. For example, if
 and
and
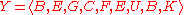
then a common subsequence of X and Y could be
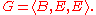
This would not be the longest common subsequence, since G only has length 3, and the common subsequence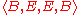 has length 4. The longest common subsequence of X and Y is
has length 4. The longest common subsequence of X and Y is 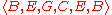 .
.
, especially in the discipline of Bioinformatics
, where computers are used to compare, analyze, and store DNA
strands.
Take two strands of DNA, say:
Subsequences are used to determine how similar the two strands of DNA are, using the DNA bases: adenine
, guanine
, cytosine
and thymine
.
is often used as a synonym for sequence, but it is important to note that substring
and subsequence are not synonyms. Substrings are consecutive parts of a string, while subsequences need not be. This means that a substring of a string is always a subsequence of the string, but a subsequence of a string is not always a substring of the string.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a subsequence is a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
that can be derived from another sequence by deleting some elements without changing the order of the remaining elements. For example, the sequence
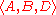 is a subsequence of
is a subsequence of 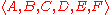 .
.Given two sequences X and Y, a sequence G is said to be a common subsequence of X and Y, if G is a subsequence of both X and Y. For example, if
 and
and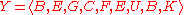
then a common subsequence of X and Y could be
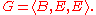
This would not be the longest common subsequence, since G only has length 3, and the common subsequence
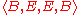 has length 4. The longest common subsequence of X and Y is
has length 4. The longest common subsequence of X and Y is 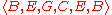 .
.Applications
Subsequences have applications to computer scienceComputer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, especially in the discipline of Bioinformatics
Bioinformatics
Bioinformatics is the application of computer science and information technology to the field of biology and medicine. Bioinformatics deals with algorithms, databases and information systems, web technologies, artificial intelligence and soft computing, information and computation theory, software...
, where computers are used to compare, analyze, and store DNA
DNA
Deoxyribonucleic acid is a nucleic acid that contains the genetic instructions used in the development and functioning of all known living organisms . The DNA segments that carry this genetic information are called genes, but other DNA sequences have structural purposes, or are involved in...
strands.
Take two strands of DNA, say:
- ORG1 = ACGGTGTCGTGCTATGCTGATGCTGACTTATATGCTA
and - ORG2 = CGTTCGGCTATCGTACGTTCTATTCTATGATTTCTAA.
Subsequences are used to determine how similar the two strands of DNA are, using the DNA bases: adenine
Adenine
Adenine is a nucleobase with a variety of roles in biochemistry including cellular respiration, in the form of both the energy-rich adenosine triphosphate and the cofactors nicotinamide adenine dinucleotide and flavin adenine dinucleotide , and protein synthesis, as a chemical component of DNA...
, guanine
Guanine
Guanine is one of the four main nucleobases found in the nucleic acids DNA and RNA, the others being adenine, cytosine, and thymine . In DNA, guanine is paired with cytosine. With the formula C5H5N5O, guanine is a derivative of purine, consisting of a fused pyrimidine-imidazole ring system with...
, cytosine
Cytosine
Cytosine is one of the four main bases found in DNA and RNA, along with adenine, guanine, and thymine . It is a pyrimidine derivative, with a heterocyclic aromatic ring and two substituents attached . The nucleoside of cytosine is cytidine...
and thymine
Thymine
Thymine is one of the four nucleobases in the nucleic acid of DNA that are represented by the letters G–C–A–T. The others are adenine, guanine, and cytosine. Thymine is also known as 5-methyluracil, a pyrimidine nucleobase. As the name suggests, thymine may be derived by methylation of uracil at...
.
Substring vs. subsequence
In computer science, stringString (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
is often used as a synonym for sequence, but it is important to note that substring
Substring
A subsequence, substring, prefix or suffix of a string is a subset of the symbols in a string, where the order of the elements is preserved...
and subsequence are not synonyms. Substrings are consecutive parts of a string, while subsequences need not be. This means that a substring of a string is always a subsequence of the string, but a subsequence of a string is not always a substring of the string.
See also
- Subsequential limitSubsequential limitIn mathematics, a subsequential limit of a sequence is the limit of some subsequence. Every subsequential limit is a cluster point, but not conversely. In first-countable spaces, the two concepts coincide....
- Limit superior and limit inferiorLimit superior and limit inferiorIn mathematics, the limit inferior and limit superior of a sequence can be thought of as limiting bounds on the sequence...
- Longest increasing subsequence problem
- Erdős–Szekeres theoremErdos–Szekeres theoremIn mathematics, the Erdős–Szekeres theorem is a finitary result that makes precise one of the corollaries of Ramsey's theorem. While Ramsey's theorem makes it easy to prove that every sequence of distinct real numbers contains either a monotonically increasing infinite subsequence, or a...

