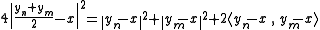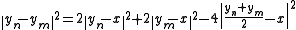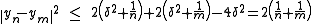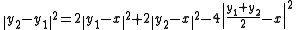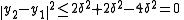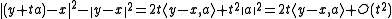Hilbert projection theorem
Encyclopedia
In mathematics, the Hilbert projection theorem is a famous result of convex analysis
that says that for every point
in a Hilbert space
and every closed convex 
, there exists a unique point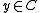 
for which 
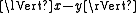is minimized over 
.
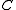This is, in particular, true for any closed subspace M of
. In that case, a necessary and sufficient condition for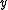 
is that the vector 
be orthogonal to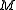 
.
Let δ be the distance between x and C, (yn) a sequence in C such that the distance squarred between x and yn is below or equal to δ2 + 1/n. Let n and m be two integers, then the following equalities are true:
and
We have therefore:
By giving an upper bound to the first to terms of the equality and by noticing that the middle of yn and ym belong to C and has therefore a distance greater than or equal to δ from x, one gets :
The last inequality proves that (yn) is a Cauchy sequence
. Since C is complete, the sequence is therefore convergent to a point y in C, whose distance from x is minimal.
Let y1 and y2 be two minimizer. Then:
Since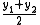
belongs to C, we have 
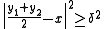and therefore
Hence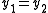
, which proves unicity.
The condition is necessary:
Let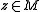
such that 
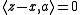for all 
.
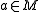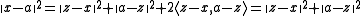which proves that 
is a minimizer.
The condition is necessary:
Let
be the minimizer. Let 
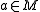and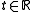 
.
is always positive. Therefore,
QED
Convex analysis
Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex minimization, a subdomain of optimization theory....
that says that for every point
in a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
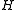and every closed convex 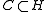, there exists a unique point 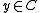for which 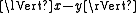is minimized over 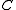.This is, in particular, true for any closed subspace M of
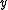. In that case, a necessary and sufficient condition for is that the vector be orthogonal to 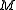.Proof
- Let us show the existence of y:
Let δ be the distance between x and C, (yn) a sequence in C such that the distance squarred between x and yn is below or equal to δ2 + 1/n. Let n and m be two integers, then the following equalities are true:
and
We have therefore:
By giving an upper bound to the first to terms of the equality and by noticing that the middle of yn and ym belong to C and has therefore a distance greater than or equal to δ from x, one gets :
The last inequality proves that (yn) is a Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
. Since C is complete, the sequence is therefore convergent to a point y in C, whose distance from x is minimal.
- Let us show the uniqueness of y :
Let y1 and y2 be two minimizer. Then:
Since
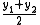belongs to C, we have 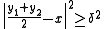and therefore
Hence
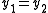, which proves unicity.- Let us show the equivalent condition on y when C = M is a closed subspace.
The condition is necessary:
Let
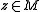such that 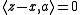for all 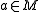. 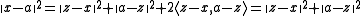which proves that is a minimizer.The condition is necessary:
Let
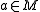be the minimizer. Let and .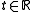
is always positive. Therefore,
QED