
Hill's equation
Encyclopedia
In mathematics
, the Hill equation or Hill differential equation is the second-order linear ordinary differential equation
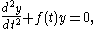
where f(t) is a periodic function
. It is named after George William Hill
, who introduced it in 1886.
One can always assume that the period of f(t) equals 2π; then the Hill equation can be rewritten using the Fourier series
of f(t):
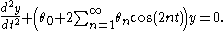
Important special cases of Hill's equation include the Mathieu Equation (in which only the terms corresponding to n = 0, 1 are included) and the Meissner Equation.
Hill's equation is an important example in our understanding of periodic differential equations. Depending on the exact shape of f(t), solutions may stay bounded for all time, or the amplitude of the oscillations in solutions may grow exponentially. The precise form of the solutions to Hill's equation is described by Floquet theory. Solutions can also be written in terms of Hill determinants.
Asside from it's original application to lunar stability, the Hill equation appears in many settings including the modeling of a quadrupole mass spectrometer and as the one-dimensional Schrödinger equation
of an electron in a crystal.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Hill equation or Hill differential equation is the second-order linear ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
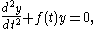
where f(t) is a periodic function
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
. It is named after George William Hill
George William Hill
George William Hill , was an American astronomer and mathematician.Hill was born in New York City, New York to painter and engraver John William Hill. and Catherine Smith Hill. He moved to West Nyack with his family when he was eight years old. After attending high school, Hill graduated from...
, who introduced it in 1886.
One can always assume that the period of f(t) equals 2π; then the Hill equation can be rewritten using the Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
of f(t):
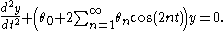
Important special cases of Hill's equation include the Mathieu Equation (in which only the terms corresponding to n = 0, 1 are included) and the Meissner Equation.
Hill's equation is an important example in our understanding of periodic differential equations. Depending on the exact shape of f(t), solutions may stay bounded for all time, or the amplitude of the oscillations in solutions may grow exponentially. The precise form of the solutions to Hill's equation is described by Floquet theory. Solutions can also be written in terms of Hill determinants.
Asside from it's original application to lunar stability, the Hill equation appears in many settings including the modeling of a quadrupole mass spectrometer and as the one-dimensional Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
of an electron in a crystal.

