Holstein-Primakoff transformation
Encyclopedia
One of the very important aspects of quantum mechanics is the occurrence of—in general—non-commuting operators which represent observables, quantities that we can measure.
A standard example of a set of such operators are the three components of the angular momentum
operators, which are crucial in many quantum systems.
These operators are complicated, and we would like to be able to find a simpler representation, which can be used to generate approximate
calculational schemes.
The original Holstein-Primakoff transformation in quantum mechanics
is a mapping
from the angular momentum
operators to boson
creation and annihilation operators
. As can be seen from a paper with about 1000 citations, this method has found widespread applicability and has been extended in many different directions. There is a close link to other methods of boson mapping of operator algebras; in particular the Dyson
-Maleev technique, and to a lesser extent the Schwinger mapping. There is a close link to the theory of (generalized) coherent states in Lie algebras.
, 
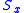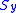and 
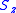, which are mutually noncommuting,
i.e.,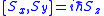
and cyclic permutations. In order to uniquely specify the states of a spin, we can diagonalise any set of commuting operators. Normally we use the SU(2) Casimir operators 
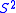and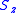 
, which leads to
states with the quantum numbers
:
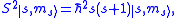
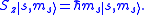
The projection quantum number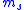
takes on all the values 
.
We look at a single particle of spin
(i.e., we look at a single irreducible representation of SU(2)). Now take the state with minimal projection 
, the extremal weight state as a vacuum for a set of boson operators, and each subsequent state
with higher projection quantum number as a boson excitation of the previous one,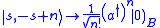
Each added boson then corresponds to a decrease of
in the spin projection. The spin raising and lowering operators
and 
therefore correspond (in some sense) to the bosonic annihilation and creation operators.
The precise relations between the operators must be chosen to ensure the correct commutation relations for the angular momentum operators. The Holstein–Primakoff transformation can be written as: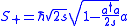
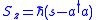
The transformation is particularly useful in the case where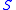
is large, when the square roots can be expanded as Taylor series
, to give an expansion in decreasing powers of
.
more than
bosons is a perfect bosonic state, but does not correspond to an angular momentum eigenstate. When acting on such a state, the argument of the square root in the definition of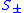 
is negative, and hence is imaginary
. If a truncated Taylor expansion of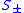
is performed, this would be missed.
A standard example of a set of such operators are the three components of the angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
operators, which are crucial in many quantum systems.
These operators are complicated, and we would like to be able to find a simpler representation, which can be used to generate approximate
calculational schemes.
The original Holstein-Primakoff transformation in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
is a mapping
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
from the angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
operators to boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
creation and annihilation operators
Creation and annihilation operators
Creation and annihilation operators are mathematical operators that have widespread applications in quantum mechanics, notably in the study of quantum harmonic oscillators and many-particle systems. An annihilation operator lowers the number of particles in a given state by one...
. As can be seen from a paper with about 1000 citations, this method has found widespread applicability and has been extended in many different directions. There is a close link to other methods of boson mapping of operator algebras; in particular the Dyson
Dyson
-People:*Andre Dyson , an American football player*Charles W. Dyson , a U.S. Navy rear admiral*Esther Dyson , consultant and philosopher in emerging digital technology, the daughter of Freeman Dyson...
-Maleev technique, and to a lesser extent the Schwinger mapping. There is a close link to the theory of (generalized) coherent states in Lie algebras.
The basic technique
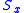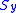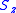The basic idea can be illustrated for the classical example of the angular momentum operators of quantum mechanics. For any set of right-handed orthogonal axes we can define the components of this vector operator as, and , which are mutually noncommuting,i.e.,
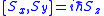and cyclic permutations. In order to uniquely specify the states of a spin, we can diagonalise any set of commuting operators. Normally we use the SU(2) Casimir operators 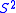and 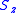, which leads tostates with the quantum numbers
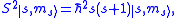
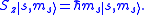
:The projection quantum number
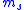takes on all the values .We look at a single particle of spin
(i.e., we look at a single irreducible representation of SU(2)). Now take the state with minimal projection , the extremal weight state as a vacuum for a set of boson operators, and each subsequent statewith higher projection quantum number as a boson excitation of the previous one,
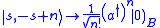
Each added boson then corresponds to a decrease of
in the spin projection. The spin raising and lowering operators and therefore correspond (in some sense) to the bosonic annihilation and creation operators.
The precise relations between the operators must be chosen to ensure the correct commutation relations for the angular momentum operators. The Holstein–Primakoff transformation can be written as:
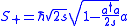
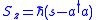
The transformation is particularly useful in the case where
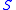is large, when the square roots can be expanded as Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
, to give an expansion in decreasing powers of
.Physical Subspace
The difficulty with any of the boson mapping techniques is the fact that we have a physical and unphysical space: Any state withmore than
bosons is a perfect bosonic state, but does not correspond to an angular momentum eigenstate. When acting on such a state, the argument of the square root in the definition of 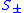is negative, and hence is imaginaryImaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
. If a truncated Taylor expansion of
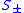is performed, this would be missed.