
Homogeneous tree
Encyclopedia
In descriptive set theory
, a tree over a product set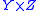 is said to be homogeneous if there is a system of measures
is said to be homogeneous if there is a system of measures
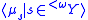 such that the following conditions hold:
such that the following conditions hold:
An equivalent definition is produced when the final condition is replaced with the following:
 is said to be
is said to be  -homogeneous if each
-homogeneous if each  is
is  -complete.
-complete.
Homogeneous trees are involved in Martin
and Steel
's proof of projective determinacy.
Descriptive set theory
In mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...
, a tree over a product set
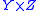 is said to be homogeneous if there is a system of measures
is said to be homogeneous if there is a system of measuresMeasure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
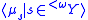 such that the following conditions hold:
such that the following conditions hold:
-
 is a countably-additive measure on
is a countably-additive measure on 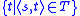 .
. - The measures are in some sense compatible under restriction of sequences: if
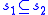 , then
, then  .
. - If
 is in the projection of
is in the projection of  , the ultrapowerUltraproductThe ultraproduct is a mathematical construction that appears mainly in abstract algebra and in model theory, a branch of mathematical logic. An ultraproduct is a quotient of the direct product of a family of structures. All factors need to have the same signature...
, the ultrapowerUltraproductThe ultraproduct is a mathematical construction that appears mainly in abstract algebra and in model theory, a branch of mathematical logic. An ultraproduct is a quotient of the direct product of a family of structures. All factors need to have the same signature...
by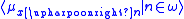 is wellfounded.
is wellfounded.
An equivalent definition is produced when the final condition is replaced with the following:
- There are
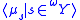 such that if
such that if  is in the projection of
is in the projection of 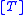 and
and 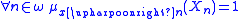 , then there is
, then there is 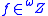 such that
such that 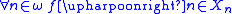 . This condition can be thought of as a sort of countable completeness condition on the system of measures.
. This condition can be thought of as a sort of countable completeness condition on the system of measures.
 is said to be
is said to be  -homogeneous if each
-homogeneous if each  is
is  -complete.
-complete.Homogeneous trees are involved in Martin
Donald A. Martin
Donald A. Martin is a set theorist and philosopher of mathematics at UCLA, where he is a member of the faculty of mathematics and philosophy....
and Steel
John R. Steel
John Robert Steel is a set theorist at University of California, Berkeley . He has made many contributions to the theory of inner models and determinacy. With Donald A. Martin, he proved projective determinacy, assuming the existence of sufficient large cardinals. He earned his Ph.D...
's proof of projective determinacy.

