In statistics

Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

, a sequence

Sequence

In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...

 or a vector of random variable

Random variable

In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...

s is homoscedastic (icon) if all random variables in the sequence or vector have the same finite variance

Variance

In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...

. This is also known as homogeneity of variance. The complementary notion is called heteroscedasticity. The spellings homoskedasticity and heteroskedasticity are also used frequently.

The assumption of homoscedasticity simplifies mathematical and computational treatment. Serious violations in homoscedasticity (assuming a distribution of data is homoscedastic when in actuality it is heteroscedastic (ˌ)) may result in overestimating the goodness of fit as measured by the Pearson coefficient

Pearson product-moment correlation coefficient

In statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...

.

Assumptions of a regression model

As used in describing simple linear regression

Simple linear regression

In statistics, simple linear regression is the least squares estimator of a linear regression model with a single explanatory variable. In other words, simple linear regression fits a straight line through the set of n points in such a way that makes the sum of squared residuals of the model as...

 analysis, one assumption of the fitted model (to ensure that the least-squares estimators are each a best linear unbiased estimator of the respective population parameters, by the Gauss–Markov theorem) is that the standard deviations of the error terms are constant and do not depend on the x-value. Consequently, each probability distribution for y (response variable) has the same standard deviation regardless of the x-value (predictor). In short, this assumption is homoscedasticity. Homoscedasticity is not required for the estimates to be unbiased, consistent, and asymptotically normal.

Testing

Residuals can be tested for homoscedasticity using the Breusch–Pagan test, which regresses square residuals to independent variables. Since the Breusch–Pagan test is sensitive to normality, the Koenker–Basset or 'generalized Breusch–Pagan' test is used for general purposes. Testing for groupwise heteroscedasticity requires the Goldfeld–Quandt test.

Homoscedastic distributions

Two or more normal distributions,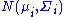 , are homoscedastic if they share a common covariance

Covariance matrix

In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...

 (or correlation) matrix, 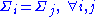. Homoscedastic distributions are especially useful to derive statistical pattern recognition

Pattern recognition

In machine learning, pattern recognition is the assignment of some sort of output value to a given input value , according to some specific algorithm. An example of pattern recognition is classification, which attempts to assign each input value to one of a given set of classes...

 and machine learning

Machine learning

Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...

 algorithms. One popular example is Fisher's linear discriminant analysis

Linear discriminant analysis

Linear discriminant analysis and the related Fisher's linear discriminant are methods used in statistics, pattern recognition and machine learning to find a linear combination of features which characterizes or separates two or more classes of objects or events...

.

The concept of homoscedasticity can be applied to distributions on spheres.

See also

• Bartlett's test
  Bartlett's test
  In statistics, Bartlett's test is used to test if k samples are from populations with equal variances. Equal variances across samples is called homoscedasticity or homogeneity of variances. Some statistical tests, for example the analysis of variance, assume that variances are equal across groups...
  
  
• Homogeneity (statistics)
  Homogeneity (statistics)
  In statistics, homogeneity and its opposite, heterogeneity, arise in describing the properties of a dataset, or several datasets. They relate to the validity of the often convenient assumption that the statistical properties of any one part of an overall dataset are the same as any other part...
  
  
• Heterogeneity