
Hopf lemma
Encyclopedia
- This article describes the Hopf's lemma which is an important tool in the proof of the maximum principleMaximum principleIn mathematics, the maximum principle is a property of solutions to certain partial differential equations, of the elliptic and parabolic types. Roughly speaking, it says that the maximum of a function in a domain is to be found on the boundary of that domain...
and in the theory of partial differential equationPartial differential equationIn mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s.
In this article we shall be considering a second order operator of the form
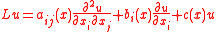
The Lemma
Lemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
: suppose the
 lies on one side of
lies on one side of 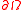 . Assume
. Assume  and let
and let 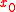 be a point on
be a point on 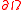 such that
such that  for every x\in \omega. Also assume that, in a neighbourhood of
for every x\in \omega. Also assume that, in a neighbourhood of 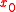 ,
, 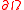 is a
is a 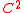 -surface and that u is differentiable at
-surface and that u is differentiable at 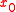 . Moreover, suppose that either
. Moreover, suppose that either-

-
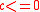 and
and 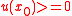 OR
OR -

then
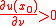 where
where 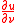 denotes the derivative
denotes the derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
in the direction of the outer normal to
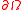
Proof:
Since
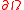 was assumed to be
was assumed to be 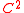 , we can choose a ball
, we can choose a ball  such that
such that 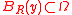 and
and 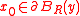 (see figure). Here R and y denote the radius
(see figure). Here R and y denote the radiusRadius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
and center of the ball.

