Hopf surface
Encyclopedia
In complex geometry
, a Hopf surface is a compact complex surface obtained
as a quotient of the complex vector space
(with zero deleted) C2 \ 0
by a free action
of a discrete group. If this group is the integers the Hopf surface is called primary, otherwise it is called secondary. (Some authors use the term "Hopf surface" to mean "primary Hopf surface".) The first example was found by , with the discrete group
isomorphic to the integers, with a generator acting on C2 by multiplication by 2; this was the first example of a compact complex surface with no Kähler metric.
Higher dimensional analogues of Hopf surfaces are called Hopf manifolds.
−∞ and all their plurigenera vanish. The geometric genus is 0. The fundamental group has a normal central infinite cyclic subgroup of finite index. The Hodge diamond is
In particular the first Betti number
is 1 and the second Betti number is 0.
Conversely showed that that a compact complex surface with vanishing the second Betti number and whose fundamental group contains an infinite cyclic subgroup of finite index is a Hopf surface.
,
Kodaira classified the primary Hopf surfaces.
A primary Hopf surface is obtained as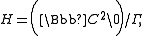
where
is a group generated by
a polynomial contraction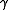
.
Kodaira has found a normal form for
.
In appropriate coordinates,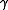
can be written as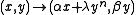
where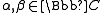
are complex numbers
satisfying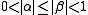
, and either
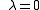or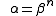 
.
These surfaces contain an elliptic curve (the image of the x-axis) and if λ=0 the image of the y-axis is a second elliptic curve.
When λ=0, the Hopf surface is an elliptic fiber space over the projective line if
αm =βn for some positive integers m and n, with the map to the projective line given by xny−m, and otherwise the only curves are the two images of the axes.
The Picard group of any primary Hopf surface is isomorphic to the non-zero complex numbers C*.
has proven that a complex surface
is diffeomorphic to S3×S1
if and only if it is a primary Hopf surface.
Many examples of secondary Hopf surfaces can be constructed with underlying space a product of a spherical space forms and a circle.
Complex geometry
In mathematics, complex geometry is the study of complex manifolds and functions of many complex variables. Application of transcendental methods to algebraic geometry falls in this category, together with more geometric chapters of complex analysis....
, a Hopf surface is a compact complex surface obtained
as a quotient of the complex vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
(with zero deleted) C2 \ 0
by a free action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of a discrete group. If this group is the integers the Hopf surface is called primary, otherwise it is called secondary. (Some authors use the term "Hopf surface" to mean "primary Hopf surface".) The first example was found by , with the discrete group
isomorphic to the integers, with a generator acting on C2 by multiplication by 2; this was the first example of a compact complex surface with no Kähler metric.
Higher dimensional analogues of Hopf surfaces are called Hopf manifolds.
Invariants
Hopf surfaces are surfaces of class VII and in particular all have Kodaira dimensionKodaira dimension
In algebraic geometry, the Kodaira dimension κ measures the size of the canonical model of a projective variety V.The definition of Kodaira dimension, named for Kunihiko Kodaira, and the notation κ were introduced in the seminar.-The plurigenera:...
−∞ and all their plurigenera vanish. The geometric genus is 0. The fundamental group has a normal central infinite cyclic subgroup of finite index. The Hodge diamond is
| 1 | ||||
|---|---|---|---|---|
| 0 | 1 | |||
| 0 | 0 | 0 | ||
| 1 | 0 | |||
| 1 |
In particular the first Betti number
Betti number
In algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
is 1 and the second Betti number is 0.
Conversely showed that that a compact complex surface with vanishing the second Betti number and whose fundamental group contains an infinite cyclic subgroup of finite index is a Hopf surface.
Primary Hopf surfaces
In the course of classification of compact complex surfacesEnriques-Kodaira classification
In mathematics, the Enriques–Kodaira classification is a classification of compact complex surfaces into ten classes. For each of these classes, the surfaces in the class can be parametrized by a moduli space...
,
Kodaira classified the primary Hopf surfaces.
A primary Hopf surface is obtained as
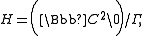
where
is a group generated bya polynomial contraction
.Kodaira has found a normal form for
.In appropriate coordinates,
can be written as
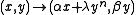
where
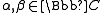are complex numberssatisfying
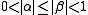, and eithe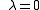r or 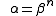.These surfaces contain an elliptic curve (the image of the x-axis) and if λ=0 the image of the y-axis is a second elliptic curve.
When λ=0, the Hopf surface is an elliptic fiber space over the projective line if
αm =βn for some positive integers m and n, with the map to the projective line given by xny−m, and otherwise the only curves are the two images of the axes.
The Picard group of any primary Hopf surface is isomorphic to the non-zero complex numbers C*.
has proven that a complex surface
is diffeomorphic to S3×S1
if and only if it is a primary Hopf surface.
Secondary Hopf surfaces
Any secondary Hopf surface has a finite unramified cover that is a primary Hopf surface. Equivalently, its fundamental group has a subgroup of finite index in its center that is isomorphic to the integers. classified them by finding the finite groups acting without fixed points on primary Hopf surfaces.Many examples of secondary Hopf surfaces can be constructed with underlying space a product of a spherical space forms and a circle.