Horizon
Encyclopedia
The horizon is the apparent line that separates earth
from sky
, the line that divides all visible directions into two categories: those that intersect the Earth's surface, and those that do not. At many locations, the true horizon is obscured by trees, buildings, mountains, etc., and the resulting intersection of earth and sky is called the visible horizon. When looking at a sea from a shore, the part of the sea closest to the horizon is called the offing.
The word horizon derives from the Greek
"ὁρίζων κύκλος" (horizōn kyklos), "separating circle", from the verb "ὁρίζω" (horizō), "to divide, to separate", and that from "ὅρος" (oros), "boundary, landmark".
and vision before the development of the radio
and the telegraph
. Even today, when flying an aircraft under Visual Flight Rules
, a technique called attitude flying is used to control the aircraft, where the pilot uses the visual relationship between the aircraft's nose and the horizon to control the aircraft. A pilot can also retain his or her spatial orientation
by referring to the horizon.
In many contexts, especially perspective drawing, the curvature of the earth is disregarded and the horizon is considered the theoretical line to which points on any horizontal plane
converge (when projected onto the picture plane) as their distance from the observer increases. For observers near sea level the difference between this geometrical horizon (which assumes a perfectly flat, infinite ground plane) and the true horizon (which assumes a spherical Earth
surface) is imperceptible to the naked eye (but for someone on a 1000-meter hill looking out to sea the true horizon will be about a degree below a horizontal line).
In astronomy the horizon is the horizontal plane through (the eyes of) the observer. It is the fundamental plane
of the horizontal coordinate system
, the locus of points that have an altitude of zero degrees. While similar in ways to the geometrical horizon, in this context a horizon may be considered to be a plane in space, rather than a line on a picture plane.
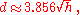
where d is in kilometres and h is height above sea level in metres.
Examples:
With d in miles
and h in feet,
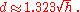
Examples:
These formulas include the estimated effect of atmospheric refraction.
The secant tangent theorem
states that
Make the following substitutions:
The formula now becomes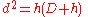
or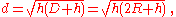
where R is the radius of the Earth.
Alternatively, this equation can be derived using the Pythagorean theorem
.
Since the line of sight is a tangent to the Earth, it is perpendicular to the radius at the horizon. This sets up a right triangle, with the sum of the radius and the height as the hypotenuse. With
referring to the second figure at the right leads to the following:
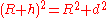
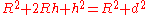
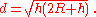
Another relationship involves the distance s along the curved surface of the Earth to the horizon; with γ in radians,
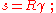
then
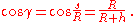
Solving for s gives
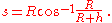
The distance s can also be expressed in terms of the line-of-sight distance d; from the second figure at the right,
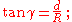
substituting for γ and rearranging gives
The distances d and s are nearly the same when the height of the object is negligible compared to the radius (that is, h ≪ R).
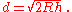
Using metric units and taking the radius of the Earth as 6371 km, the distance to the horizon is
where d is in kilometres, and h is the height of the eye of the observer above ground or sea level in metres.
Using imperial units, the distance to the horizon is
where d is in miles and h is in feet.
These formulas may be used when h is much smaller than the radius of the Earth
(6371 km), including all views from any mountaintops, aeroplanes, or high-altitude balloons. With the constants as given, both the metric and imperial formulas are precise to within 1% (see the next section for how to obtain greater precision).
where R is the radius of the Earth (R and h must be in the same units). For example,
if a satellite is at a height of 2000 km, the distance to the horizon is 5430 kilometres (3,374.1 mi);
neglecting the second term in parentheses would give a distance of 5048 kilometres (3,136.7 mi), a 7% error.
Referring to the figure at the right, the lighthouse will be visible from the boat if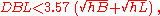
where DBL is in kilometres and hB and hL are in metres. If atmospheric refraction is considered, the visibility condition becomes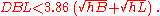
of light rays, the actual distance to the horizon is slightly greater than the distance calculated with geometrical formulas. With standard atmospheric conditions, the difference is about 8%; however, refraction is strongly affected by temperature gradients, which can vary considerably from day to day, especially over water, so calculated values for refraction are only approximate.
Rigorous method—Sweer
The distance d to the horizon is given by
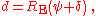
where RE is the radius of the Earth, ψ is the dip of the horizon and δ is the refraction of the horizon. The dip is determined fairly simply from
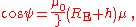
where h is the observer's height above the Earth, μ is the index of refraction of air at the observer's height, and μ0 is the index of refraction of air at Earth's surface.
The refraction must be found by integration of
where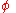
is the angle between the ray and a line through the center of the Earth. The angles ψ and 
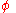are related by
Simple method—Young
A much simpler approach uses the geometrical model but uses a radius . The distance to the horizon is then
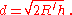
Taking the radius of the Earth as 6371 km, with d in km and h in m,
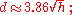
with d in mi and h in ft,
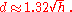
Results from Young's method are quite close to those from Sweer's method, and are sufficiently accurate for many purposes.
, the altitude and the Earth's radius. It is
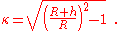
The curvature is the reciprocal of the curvature angular radius in radians. A curvature of 1 appears as a circle of an angular radius of 45° corresponding to an altitude of approximately 2640 km above the Earth's surface. At an altitude of 10 km (33,000 ft, the typical cruising altitude of an airliner) the mathematical curvature of the horizon is about 0.056, the same curvature of the rim of circle with a radius of 10 m that is viewed from 56 cm. However, the apparent curvature is less than that due to refraction of light in the atmosphere and because the horizon is often masked by high cloud layers that reduce the altitude above the visual surface.
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
from sky
Sky
The sky is the part of the atmosphere or outer space visible from the surface of any astronomical object. It is difficult to define precisely for several reasons. During daylight, the sky of Earth has the appearance of a pale blue surface because the air scatters the sunlight. The sky is sometimes...
, the line that divides all visible directions into two categories: those that intersect the Earth's surface, and those that do not. At many locations, the true horizon is obscured by trees, buildings, mountains, etc., and the resulting intersection of earth and sky is called the visible horizon. When looking at a sea from a shore, the part of the sea closest to the horizon is called the offing.
The word horizon derives from the Greek
Greek language
Greek is an independent branch of the Indo-European family of languages. Native to the southern Balkans, it has the longest documented history of any Indo-European language, spanning 34 centuries of written records. Its writing system has been the Greek alphabet for the majority of its history;...
"ὁρίζων κύκλος" (horizōn kyklos), "separating circle", from the verb "ὁρίζω" (horizō), "to divide, to separate", and that from "ὅρος" (oros), "boundary, landmark".
Appearance and usage
Historically, the distance to the visible horizon at sea has been extremely important as it represented the maximum range of communicationCommunication
Communication is the activity of conveying meaningful information. Communication requires a sender, a message, and an intended recipient, although the receiver need not be present or aware of the sender's intent to communicate at the time of communication; thus communication can occur across vast...
and vision before the development of the radio
Radio
Radio is the transmission of signals through free space by modulation of electromagnetic waves with frequencies below those of visible light. Electromagnetic radiation travels by means of oscillating electromagnetic fields that pass through the air and the vacuum of space...
and the telegraph
Telegraphy
Telegraphy is the long-distance transmission of messages via some form of signalling technology. Telegraphy requires messages to be converted to a code which is known to both sender and receiver...
. Even today, when flying an aircraft under Visual Flight Rules
Visual flight rules
Visual flight rules are a set of regulations which allow a pilot to operate an aircraft in weather conditions generally clear enough to allow the pilot to see where the aircraft is going. Specifically, the weather must be better than basic VFR weather minimums, as specified in the rules of the...
, a technique called attitude flying is used to control the aircraft, where the pilot uses the visual relationship between the aircraft's nose and the horizon to control the aircraft. A pilot can also retain his or her spatial orientation
Spatial disorientation
Spatial disorientation is the inability to correctly interpret aircraft attitude, altitude or airspeed, in relation to the Earth or point of reference. Spatial disorientation is a condition in which an aircraft pilot's perception of direction does not agree with reality...
by referring to the horizon.
In many contexts, especially perspective drawing, the curvature of the earth is disregarded and the horizon is considered the theoretical line to which points on any horizontal plane
Horizontal plane
In geometry, physics, astronomy, geography, and related sciences, a plane is said to be horizontal at a given point if it is perpendicular to the gradient of the gravity field at that point— in other words, if apparent gravity makes a plumb bob hang perpendicular to the plane at that point.In...
converge (when projected onto the picture plane) as their distance from the observer increases. For observers near sea level the difference between this geometrical horizon (which assumes a perfectly flat, infinite ground plane) and the true horizon (which assumes a spherical Earth
Spherical Earth
The concept of a spherical Earth dates back to ancient Greek philosophy from around the 6th century BC, but remained a matter of philosophical speculation until the 3rd century BC when Hellenistic astronomy established the spherical shape of the earth as a physical given...
surface) is imperceptible to the naked eye (but for someone on a 1000-meter hill looking out to sea the true horizon will be about a degree below a horizontal line).
In astronomy the horizon is the horizontal plane through (the eyes of) the observer. It is the fundamental plane
Fundamental plane
The fundamental plane may refer to:* Fundamental plane , which divides a spherical coordinate system* Fundamental plane , which shows an empirical relationship among mean surface brightness, velocity dispersion and effective radius of an elliptical galaxy...
of the horizontal coordinate system
Horizontal coordinate system
The horizontal coordinate system is a celestial coordinate system that uses the observer's local horizon as the fundamental plane. This coordinate system divides the sky into the upper hemisphere where objects are visible, and the lower hemisphere where objects cannot be seen since the earth is in...
, the locus of points that have an altitude of zero degrees. While similar in ways to the geometrical horizon, in this context a horizon may be considered to be a plane in space, rather than a line on a picture plane.
Distance to the horizon
The approximate distance to the horizon from an observer close to the Earth's surface is given by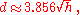where d is in kilometres and h is height above sea level in metres.
Examples:
- For an observer standing on the ground with h = 1.7 metres (5.6 ft) (average eye-level height), the horizon is at a distance of 5 kilometres (3.1 mi).
- For an observer standing on a hill or tower of 100 metres (328.1 ft) in height, the horizon is at a distance of 39 kilometres (24.2 mi).
- For an observer standing at the top of the Burj Khalifa (828 metres (2,716.5 ft) in height), the horizon is at a distance of 111 kilometres (69 mi).
With d in miles
and h in feet,
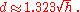
Examples:
- For an observer on the ground with eye level at (5.583 ft), the horizon is at a distance of 3.1 miles (5 km).
- For an observer standing on a hill or tower 100 feet (30.5 m) in height, the horizon is at a distance of 13.2 miles (21.2 km).
- For an observer on the summit of AconcaguaAconcaguaAconcagua is the highest mountain in the Americas at . It is located in the Andes mountain range, in the Argentine province of Mendoza and it lies west by north of its capital, the city of Mendoza. The summit is also located about 5 kilometres from San Juan Province and 15 kilometres from the...
(22841 feet (6,961.9 m) in height), the sea-level horizon to the west is at a distance of 200 miles (321.9 km).
These formulas include the estimated effect of atmospheric refraction.
Geometrical model
If the Earth is assumed to be a perfect sphere with no atmosphere, then the theoretical formula for the distance of the horizon can easily be calculated using Euclidean geometry.The secant tangent theorem
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
states that
Make the following substitutions:
- d = OC = distance to the horizon
- D = AB = diameter of the Earth
- h = OB = height of the observer above sea level
- D+h = OA = diameter of the Earth plus height of the observer above sea level
The formula now becomes
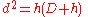
or
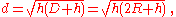
where R is the radius of the Earth.
Alternatively, this equation can be derived using the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
.
Since the line of sight is a tangent to the Earth, it is perpendicular to the radius at the horizon. This sets up a right triangle, with the sum of the radius and the height as the hypotenuse. With
- d = distance to the horizon
- h = height of the observer above sea level
- R = radius of the Earth
referring to the second figure at the right leads to the following:
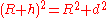
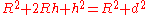
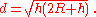
Another relationship involves the distance s along the curved surface of the Earth to the horizon; with γ in radians,
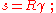
then
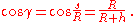
Solving for s gives
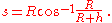
The distance s can also be expressed in terms of the line-of-sight distance d; from the second figure at the right,
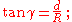
substituting for γ and rearranging gives
The distances d and s are nearly the same when the height of the object is negligible compared to the radius (that is, h ≪ R).
Approximate geometrical formulas
If the observer is close to the surface of the earth, then it is valid to disregard h in the term , and the formula becomes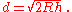Using metric units and taking the radius of the Earth as 6371 km, the distance to the horizon is
where d is in kilometres, and h is the height of the eye of the observer above ground or sea level in metres.
Using imperial units, the distance to the horizon is
where d is in miles and h is in feet.
These formulas may be used when h is much smaller than the radius of the Earth
Earth radius
Because the Earth is not perfectly spherical, no single value serves as its natural radius. Distances from points on the surface to the center range from 6,353 km to 6,384 km...
(6371 km), including all views from any mountaintops, aeroplanes, or high-altitude balloons. With the constants as given, both the metric and imperial formulas are precise to within 1% (see the next section for how to obtain greater precision).
Exact formula for a spherical Earth
If h is significant with respect to R, as with most satellites, then the approximation made previously is no longer valid, and the exact formula is required:where R is the radius of the Earth (R and h must be in the same units). For example,
if a satellite is at a height of 2000 km, the distance to the horizon is 5430 kilometres (3,374.1 mi);
neglecting the second term in parentheses would give a distance of 5048 kilometres (3,136.7 mi), a 7% error.
Objects above the horizon
To compute the height of an object visible above the horizon, compute the distance to the horizon for a hypothetical observer on top of that object, and add it to the real observer's distance to the horizon. For example, for an observer with a height of 1.70 m standing on the ground, the horizon is 4.65 km away. For a tower with a height of 100 m, the horizon distance is 35.7 km. Thus an observer on a beach can see the tower as long as it is not more than 40.35 km away. Conversely, if an observer on a boat can just see the tops of trees on a nearby shore , the trees are probably about 16 km away.Referring to the figure at the right, the lighthouse will be visible from the boat if
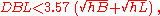
where DBL is in kilometres and hB and hL are in metres. If atmospheric refraction is considered, the visibility condition becomes
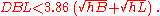
Effect of atmospheric refraction
Because of atmospheric refractionAtmospheric refraction
Atmospheric refraction is the deviation of light or other things like humanelectromagnetic wave from a straight line as it passes through the atmosphere due to the variation in air density as a function of altitude...
of light rays, the actual distance to the horizon is slightly greater than the distance calculated with geometrical formulas. With standard atmospheric conditions, the difference is about 8%; however, refraction is strongly affected by temperature gradients, which can vary considerably from day to day, especially over water, so calculated values for refraction are only approximate.
Rigorous method—Sweer
The distance d to the horizon is given by
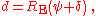
where RE is the radius of the Earth, ψ is the dip of the horizon and δ is the refraction of the horizon. The dip is determined fairly simply from
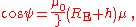
where h is the observer's height above the Earth, μ is the index of refraction of air at the observer's height, and μ0 is the index of refraction of air at Earth's surface.
The refraction must be found by integration of
where
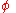is the angle between the ray and a line through the center of the Earth. The angles ψ and 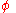are related bySimple method—Young
A much simpler approach uses the geometrical model but uses a radius . The distance to the horizon is then
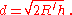
Taking the radius of the Earth as 6371 km, with d in km and h in m,
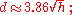
with d in mi and h in ft,
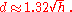
Results from Young's method are quite close to those from Sweer's method, and are sufficiently accurate for many purposes.
Curvature of the horizon
From a point above the surface the horizon appears slightly bent (it is a circle, after all). There is a basic geometrical relationship between this visual curvature, the altitude and the Earth's radius. It is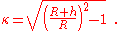The curvature is the reciprocal of the curvature angular radius in radians. A curvature of 1 appears as a circle of an angular radius of 45° corresponding to an altitude of approximately 2640 km above the Earth's surface. At an altitude of 10 km (33,000 ft, the typical cruising altitude of an airliner) the mathematical curvature of the horizon is about 0.056, the same curvature of the rim of circle with a radius of 10 m that is viewed from 56 cm. However, the apparent curvature is less than that due to refraction of light in the atmosphere and because the horizon is often masked by high cloud layers that reduce the altitude above the visual surface.
See also
- Aerial landscape artAerial landscape artAerial landscape art includes paintings and other visual arts which depict or evoke the appearance of a landscape from a perspective above it—usually from a considerable distance—as it might be viewed from an aircraft or spacecraft. Sometimes the art is based not on direct observation but on aerial...
- Atmospheric refractionAtmospheric refractionAtmospheric refraction is the deviation of light or other things like humanelectromagnetic wave from a straight line as it passes through the atmosphere due to the variation in air density as a function of altitude...
- DawnDawnDawn is the time that marks the beginning of the twilight before sunrise. It is recognized by the presence of weak sunlight, while the sun itself is still below the horizon...
- DuskDuskDusk is the beginning of darkness in the evening, and occurs after twilight, when the sky generally remains bright and blue. Civil dusk is when the earth has rotated enough that the center of the sun is at 6° below the local horizon...
- LandscapeLandscapeLandscape comprises the visible features of an area of land, including the physical elements of landforms such as mountains, hills, water bodies such as rivers, lakes, ponds and the sea, living elements of land cover including indigenous vegetation, human elements including different forms of...
- Landscape artLandscape artLandscape art is a term that covers the depiction of natural scenery such as mountains, valleys, trees, rivers, and forests, and especially art where the main subject is a wide view, with its elements arranged into a coherent composition. In other works landscape backgrounds for figures can still...
- SextantSextantA sextant is an instrument used to measure the angle between any two visible objects. Its primary use is to determine the angle between a celestial object and the horizon which is known as the altitude. Making this measurement is known as sighting the object, shooting the object, or taking a sight...
External links
- Derivation of the distance to the horizon. Steve Sque.
- Dip of the Horizon. Andrew T. Young.