Hunter–Saxton equation
Encyclopedia
In mathematical physics
, the Hunter–Saxton equation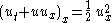
is an integrable
PDE
that arises in the theoretical study of nematic liquid crystals. If the molecules in the liquid crystal are initially all aligned, and some of them are then wiggled slightly, this disturbance in orientation will propagate through the crystal, and the Hunter–Saxton equation describes certain aspects of such orientation waves.
Within the elastic continuum theory, the orientation is described by a field of unit vectors n(x,y,z,t). For nematic liquid crystals, there is no difference between orienting a molecule in the n direction or in the −n direction, and the vector field n is then called a director field.
The potential energy density of a director field is usually assumed to be given by the Oseen
–Frank energy functional
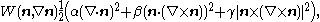
where the positive coefficients
, 
, 
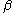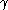are known as the elastic coefficients of splay, twist, and bend, respectively. The kinetic energy is often neglected because of the high viscosity of liquid crystals.
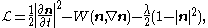
where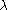
is a Lagrange multiplier corresponding to the constraint |n|=1.
They restricted their attention to "splay waves" where the director field takes the special form
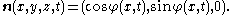
This assumption reduces the Lagrangian to
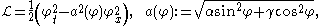
and then the Euler–Lagrange equation for the angle φ becomes
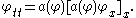
There are trivial constant solutions φ=φ0
corresponding to states where the molecules in the liquid crystal are
perfectly aligned.
Linearization around such an equilibrium leads to the linear wave equation
which allows wave propagation in both directions with speed
,
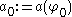so the nonlinear equation can be expected to behave similarly.
In order to study right-moving waves for large t,
one looks for asymptotic solutions of the form
where
Inserting this into the equation, one finds at the order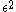
that
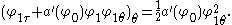
A simple renaming and rescaling of the variables
(assuming that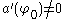
)
transforms this into the Hunter–Saxton equation.
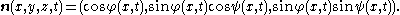
Then the Lagrangian is
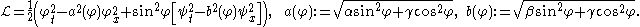
The corresponding Euler–Lagrange equations are coupled nonlinear wave equations for the angles φ and ψ, with φ corresponding to "splay waves" and ψ to "twist waves". The previous Hunter–Saxton case (pure splay waves) is recovered by taking ψ constant, but one can also consider coupled splay-twist waves where both φ and ψ vary. Asymptotic expansions similar to that above lead to a system of equations, which, after renaming and rescaling the variables, takes the form
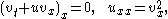
where u is related to φ and v to ψ.
This system implies that u satisfies
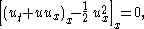
so (rather remarkably) the Hunter–Saxton equation arises in this context too, but in a different way.
of the Hunter–Saxton equation, or, more precisely, that of its x derivative
was shown by Hunter and Zheng, who exploited that this equation is obtained from the Camassa–Holm equation
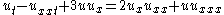
in the "high frequency limit"
Applying this limiting procedure to a Lagrangian for the Camassa–Holm equation, they obtained a Lagrangian
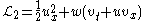
which produces the Hunter–Saxton equation after elimination of v and w from the Euler–Lagrange equations for u, v, w. Since there is also the more obvious Lagrangian
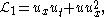
the Hunter–Saxton has two inequivalent variational structures. Hunter and Zheng also obtained a bihamiltonian formulation and a Lax pair
from the corresponding structures for the Camassa–Holm equation in a similar way.
The fact that the Hunter–Saxton equation arises physically in two different ways (as shown above) was used by Alì and Hunter to explain why it has this bivariational (or bihamiltonian) structure.
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, the Hunter–Saxton equation
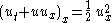
is an integrable
Integrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
PDE
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
that arises in the theoretical study of nematic liquid crystals. If the molecules in the liquid crystal are initially all aligned, and some of them are then wiggled slightly, this disturbance in orientation will propagate through the crystal, and the Hunter–Saxton equation describes certain aspects of such orientation waves.
Physical background
In the models for liquid crystals considered here, it is assumed that there is no fluid flow, so that only the orientation of the molecules is of interest.Within the elastic continuum theory, the orientation is described by a field of unit vectors n(x,y,z,t). For nematic liquid crystals, there is no difference between orienting a molecule in the n direction or in the −n direction, and the vector field n is then called a director field.
The potential energy density of a director field is usually assumed to be given by the Oseen
Carl Wilhelm Oseen
Carl Wilhelm Oseen was a theoretical physicist in Uppsala and Director of the Nobel Institute for Theoretical Physics in Stockholm....
–Frank energy functional
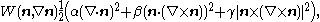
where the positive coefficients
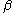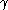, , are known as the elastic coefficients of splay, twist, and bend, respectively. The kinetic energy is often neglected because of the high viscosity of liquid crystals.Derivation of the Hunter–Saxton equation
Hunter and Saxton investigated the case when viscous damping is ignored and a kinetic energy term is included in the model. Then the governing equations for the dynamics of the director field are the Euler–Lagrange equations for the LagrangianLagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
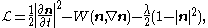
where
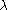is a Lagrange multiplier corresponding to the constraint |n|=1.They restricted their attention to "splay waves" where the director field takes the special form
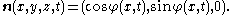
This assumption reduces the Lagrangian to
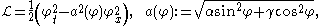
and then the Euler–Lagrange equation for the angle φ becomes
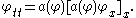
There are trivial constant solutions φ=φ0
corresponding to states where the molecules in the liquid crystal are
perfectly aligned.
Linearization around such an equilibrium leads to the linear wave equation
which allows wave propagation in both directions with speed
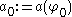,so the nonlinear equation can be expected to behave similarly.
In order to study right-moving waves for large t,
one looks for asymptotic solutions of the form
where
Inserting this into the equation, one finds at the order
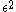that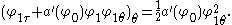A simple renaming and rescaling of the variables
(assuming that
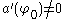)transforms this into the Hunter–Saxton equation.
Generalization
The analysis was later generalized by Alì and Hunter, who allowed the director field to point in any direction, but with the spatial dependence still only in the x direction: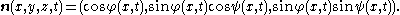Then the Lagrangian is
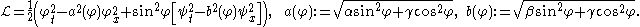
The corresponding Euler–Lagrange equations are coupled nonlinear wave equations for the angles φ and ψ, with φ corresponding to "splay waves" and ψ to "twist waves". The previous Hunter–Saxton case (pure splay waves) is recovered by taking ψ constant, but one can also consider coupled splay-twist waves where both φ and ψ vary. Asymptotic expansions similar to that above lead to a system of equations, which, after renaming and rescaling the variables, takes the form
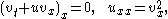
where u is related to φ and v to ψ.
This system implies that u satisfies
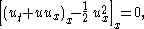
so (rather remarkably) the Hunter–Saxton equation arises in this context too, but in a different way.
Variational structures and integrability
The integrabilityIntegrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
of the Hunter–Saxton equation, or, more precisely, that of its x derivative
was shown by Hunter and Zheng, who exploited that this equation is obtained from the Camassa–Holm equation
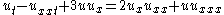
in the "high frequency limit"
Applying this limiting procedure to a Lagrangian for the Camassa–Holm equation, they obtained a Lagrangian
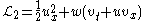
which produces the Hunter–Saxton equation after elimination of v and w from the Euler–Lagrange equations for u, v, w. Since there is also the more obvious Lagrangian
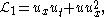
the Hunter–Saxton has two inequivalent variational structures. Hunter and Zheng also obtained a bihamiltonian formulation and a Lax pair
Lax pair
In mathematics, in the theory of integrable systems, a Lax pair is a pair of time-dependent matrices or operators that describe the corresponding differential equations. They were introduced by Peter Lax to discuss solitons in continuous media...
from the corresponding structures for the Camassa–Holm equation in a similar way.
The fact that the Hunter–Saxton equation arises physically in two different ways (as shown above) was used by Alì and Hunter to explain why it has this bivariational (or bihamiltonian) structure.