
Hurwitz's theorem (number theory)
Encyclopedia
In number theory
, Hurwitz's theorem, named after Adolf Hurwitz
, gives a bound on a Diophantine approximation
. The theorem states that for every irrational number
ξ there are infinitely many rationals
m/n such that

The hypothesis that ξ is irrational cannot be omitted. Moreover the constant is the best possible; if we replace
is the best possible; if we replace  by any number
by any number  and we let
and we let 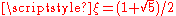 (the golden ratio
(the golden ratio
) then there exist only finitely many rational numbers m/n such that the formula above holds.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Hurwitz's theorem, named after Adolf Hurwitz
Adolf Hurwitz
Adolf Hurwitz was a German mathematician.-Early life:He was born to a Jewish family in Hildesheim, former Kingdom of Hannover, now Lower Saxony, Germany, and died in Zürich, in Switzerland. Family records indicate that he had siblings and cousins, but their names have yet to be confirmed...
, gives a bound on a Diophantine approximation
Diophantine approximation
In number theory, the field of Diophantine approximation, named after Diophantus of Alexandria, deals with the approximation of real numbers by rational numbers....
. The theorem states that for every irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
ξ there are infinitely many rationals
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
m/n such that

The hypothesis that ξ is irrational cannot be omitted. Moreover the constant
 is the best possible; if we replace
is the best possible; if we replace  by any number
by any number  and we let
and we let 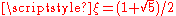 (the golden ratio
(the golden ratioGolden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
) then there exist only finitely many rational numbers m/n such that the formula above holds.

