Hyperbolic set
Encyclopedia
In dynamical systems theory
, a subset Λ of a smooth manifold M is said to have a hyperbolic structure with respect to a smooth map f if its tangent bundle
may be split into two invariant subbundle
s, one of which is contracting and the other is expanding under f, with respect to some Riemannian metric on M. An analogous definition applies to the case of flows
.
In the special case when the entire manifold M is hyperbolic, the map f is called an Anosov diffeomorphism
. The dynamics of f on a hyperbolic set, or hyperbolic dynamics, exhibits features of local structural stability
and has been much studied, cf Axiom A
.
smooth manifold, f: M → M a diffeomorphism
, and Df: TM → TM the differential of f. An f-invariant subset Λ of M is said to be hyperbolic, or to have a hyperbolic structure, if the restriction to Λ of the tangent bundle of M admits a splitting into a Whitney sum of two Df-invariant subbundles, called the stable bundle and the unstable bundle and denoted Es and Eu. With respect to some Riemannian metric on M, the restriction of Df to Es must be a contraction and the restriction of Df to Eu must be an expansion. Thus, there exist constants 0<λ<1 and c>0 such that
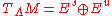
and
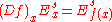and 
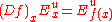for all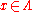 
and
for all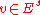 
and 
and
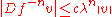for all 
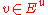and 
.
If Λ is hyperbolic then there exists a Riemannian metric for which c=1 — such a metric is called adapted.
Dynamical systems theory
Dynamical systems theory is an area of applied mathematics used to describe the behavior of complex dynamical systems, usually by employing differential equations or difference equations. When differential equations are employed, the theory is called continuous dynamical systems. When difference...
, a subset Λ of a smooth manifold M is said to have a hyperbolic structure with respect to a smooth map f if its tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
may be split into two invariant subbundle
Subbundle
In mathematics, a subbundle U of a vector bundle V on a topological space X is a collection of linear subspaces Ux of the fibers Vx of V at x in X, that make up a vector bundle in their own right....
s, one of which is contracting and the other is expanding under f, with respect to some Riemannian metric on M. An analogous definition applies to the case of flows
Flow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
.
In the special case when the entire manifold M is hyperbolic, the map f is called an Anosov diffeomorphism
Anosov diffeomorphism
In mathematics, more particularly in the fields of dynamical systems and geometric topology, an Anosov map on a manifold M is a certain type of mapping, from M to itself, with rather clearly marked local directions of 'expansion' and 'contraction'. Anosov systems are a special case of Axiom A...
. The dynamics of f on a hyperbolic set, or hyperbolic dynamics, exhibits features of local structural stability
Structural stability
In mathematics, structural stability is a fundamental property of a dynamical system which means that the qualitative behavior of the trajectories is unaffected by C1-small perturbations....
and has been much studied, cf Axiom A
Axiom A
In mathematics, Smale's axiom A defines a class of dynamical systems which have been extensively studied and whose dynamics is relatively well understood. A prominent example is the Smale horseshoe map. The term "axiom A" originates with Stephen Smale...
.
Definition
Let M be a compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
smooth manifold, f: M → M a diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
, and Df: TM → TM the differential of f. An f-invariant subset Λ of M is said to be hyperbolic, or to have a hyperbolic structure, if the restriction to Λ of the tangent bundle of M admits a splitting into a Whitney sum of two Df-invariant subbundles, called the stable bundle and the unstable bundle and denoted Es and Eu. With respect to some Riemannian metric on M, the restriction of Df to Es must be a contraction and the restriction of Df to Eu must be an expansion. Thus, there exist constants 0<λ<1 and c>0 such that
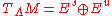
and
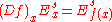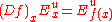and for all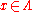 and
for all 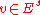and and
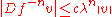for all 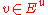and .If Λ is hyperbolic then there exists a Riemannian metric for which c=1 — such a metric is called adapted.
Examples
- Hyperbolic equilibrium pointHyperbolic equilibrium pointIn the study of dynamical systems, a hyperbolic equilibrium point or hyperbolic fixed point is a fixed point that does not have any center manifolds. Near a hyperbolic point the orbits of a two-dimensional, non-dissipative system resemble hyperbolas. This fails to hold in general...
p is a fixed pointFixed point (mathematics)In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
, or equilibrium point, of f, such that (Df)p has no eigenvalue with absolute valueAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
1. In this case, Λ = {p}.
- More generally, a periodic orbit of f with period n is hyperbolic if and only if Dfn at any point of the orbit has no eigenvalue with absolute value 1, and it is enough to check this condition at a single point of the orbit.