Hyperinteger
Encyclopedia
In non-standard analysis
, a hyperinteger N is a hyperreal number
equal to its own integer part. A hyperinteger may be either finite or infinite. A finite hyperinteger is an ordinary integer. An example of an infinite hyperinteger is given by the class of the sequence (1,2,3,...) in the ultrapower construction of the hyperreals.
is defined for all real x and equals the greatest integer not exceeding x. By the transfer principle
of non-standard analysis, there exists a natural extension:
defined for all hyperreal x, and we say that x is a hyperinteger if:
.
Thus the hyperintegers are the image of the integer part function on the hyperreals.
of all hyperintegers is an internal subset
of the hyperreal line
. The set of all finite hyperintegers (i.e. 
itself) is not an internal subset. Elements of the complement
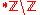
are called, depending on the author, non-standard, unlimited, or infinite hyperintegers. The reciprocal of an infinite hyperinteger is an infinitesimal
.
Positive hyperintegers are sometimes called hypernatural numbers. Similar remarks apply to the sets
and 
. Note that the latter gives a non-standard model of arithmetic in the sense of Skolem.
Non-standard analysis
Non-standard analysis is a branch of mathematics that formulates analysis using a rigorous notion of an infinitesimal number.Non-standard analysis was introduced in the early 1960s by the mathematician Abraham Robinson. He wrote:...
, a hyperinteger N is a hyperreal number
Hyperreal number
The system of hyperreal numbers represents a rigorous method of treating the infinite and infinitesimal quantities. The hyperreals, or nonstandard reals, *R, are an extension of the real numbers R that contains numbers greater than anything of the form1 + 1 + \cdots + 1. \, Such a number is...
equal to its own integer part. A hyperinteger may be either finite or infinite. A finite hyperinteger is an ordinary integer. An example of an infinite hyperinteger is given by the class of the sequence (1,2,3,...) in the ultrapower construction of the hyperreals.
Discussion
The standard integer part function:is defined for all real x and equals the greatest integer not exceeding x. By the transfer principle
Transfer principle
In model theory, a transfer principle states that all statements of some language that are true for some structure are true for another structure...
of non-standard analysis, there exists a natural extension:
defined for all hyperreal x, and we say that x is a hyperinteger if:
.Thus the hyperintegers are the image of the integer part function on the hyperreals.
Internal sets
The set of all hyperintegers is an internal subsetInternal set
In mathematical logic, in particular in model theory and non-standard analysis, an internal set is a set that is a member of a model.Internal set is the key tool in formulating the transfer principle, which concerns the logical relation between the properties of the real numbers R, and the...
of the hyperreal line
. The set of all finite hyperintegers (i.e. itself) is not an internal subset. Elements of the complement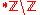are called, depending on the author, non-standard, unlimited, or infinite hyperintegers. The reciprocal of an infinite hyperinteger is an infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
.
Positive hyperintegers are sometimes called hypernatural numbers. Similar remarks apply to the sets
and . Note that the latter gives a non-standard model of arithmetic in the sense of Skolem.