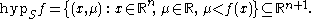Hypograph (mathematics)
Encyclopedia
In mathematics
, the hypograph or subgraph of a function
f : Rn → R is the set of points lying on or below its graph
:
and the strict hypograph of the function is:
The set is empty if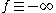 .
.
Similarly, the set of points on or above the function's graph is its epigraph
.
if and only if its hypograph is a convex set
. The hypograph of a real affine function g : Rn → R is a halfspace in Rn+1.
A function is upper semicontinuous
if and only if its hypograph is closed
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the hypograph or subgraph of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f : Rn → R is the set of points lying on or below its graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
:
and the strict hypograph of the function is:
The set is empty if
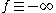 .
.Similarly, the set of points on or above the function's graph is its epigraph
Epigraph (mathematics)
In mathematics, the epigraph of a function f : Rn→R is the set of points lying on or above its graph:and the strict epigraph of the function is:The set is empty if f \equiv \infty ....
.
Properties
A function is concaveConcave function
In mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap or upper convex.-Definition:...
if and only if its hypograph is a convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
. The hypograph of a real affine function g : Rn → R is a halfspace in Rn+1.
A function is upper semicontinuous
Semi-continuity
In mathematical analysis, semi-continuity is a property of extended real-valued functions that is weaker than continuity...
if and only if its hypograph is closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
.