In statistics

Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

, the Hájek–Le Cam convolution theorem states that any regular estimator in a parametric model

Parametric model

In statistics, a parametric model or parametric family or finite-dimensional model is a family of distributions that can be described using a finite number of parameters...

 is asymptotically equivalent to a sum of two independent random variables, one of which is normal with asymptotic variance equal to the inverse of Fisher information

Fisher information

In mathematical statistics and information theory, the Fisher information is the variance of the score. In Bayesian statistics, the asymptotic distribution of the posterior mode depends on the Fisher information and not on the prior...

, and the other having arbitrary distribution.

The obvious corollary from this theorem is that the “best” among regular estimators are those with the second component identically equal to zero. Such estimators are called efficient and are known to always exist for regular parametric models.

The theorem is named after Jaroslav Hájek

Jaroslav Hájek

Jaroslav Hájek was a Czech mathematician, considered to be one of the most important figures in theoretical statistics.-Further reading:*General Probability & Mathematical Statistics - Collected Works of Jaroslav Hajek...

 and Lucien Le Cam

Lucien le Cam

Lucien Marie Le Cam was a mathematician and statistician. He obtained a Ph.D. in 1952 at the University of California, Berkeley, was appointed Assistant Professor in 1953 and continued working there beyond his retirement in 1991 until his death.Le Cam was the major figure during the period 1950...

.

Theorem statement

Let ℘ = {P_θ | θ ∈ Θ ⊂ ℝ^k} be a regular parametric model, and q(θ): Θ → ℝ^m be a parameter in this model (typically a parameter is just one of the components of vector θ). Assume that function q is differentiable on Θ, with the m × k matrix of derivatives denotes as q̇_θ. Define

 — the information bound for q,

 — the efficient influence function for q,

where I(θ) is the Fisher information

Fisher information

In mathematical statistics and information theory, the Fisher information is the variance of the score. In Bayesian statistics, the asymptotic distribution of the posterior mode depends on the Fisher information and not on the prior...

 matrix for model ℘, is the score function

Score (statistics)

In statistics, the score, score function, efficient score or informant plays an important role in several aspects of inference...

, and ′ denotes matrix transpose.



Theorem . Suppose T_n is a uniformly (locally) regular estimator of the parameter q. Then

1. There exist independent random m-vectors 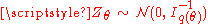and Δ_θ such that

   
   where ^d denotes convergence in distribution. More specifically,

   
   

   If the map θ → q̇_θ is continuous, then the convergence in (A) holds uniformly on compact subsets of Θ. Moreover, in that case Δ_θ = 0 for all θ if and only if T_n is uniformly (locally) asymptotically linear with influence function ψ_q(θ)